话不多说,我们上题目:
方法一:动态规划
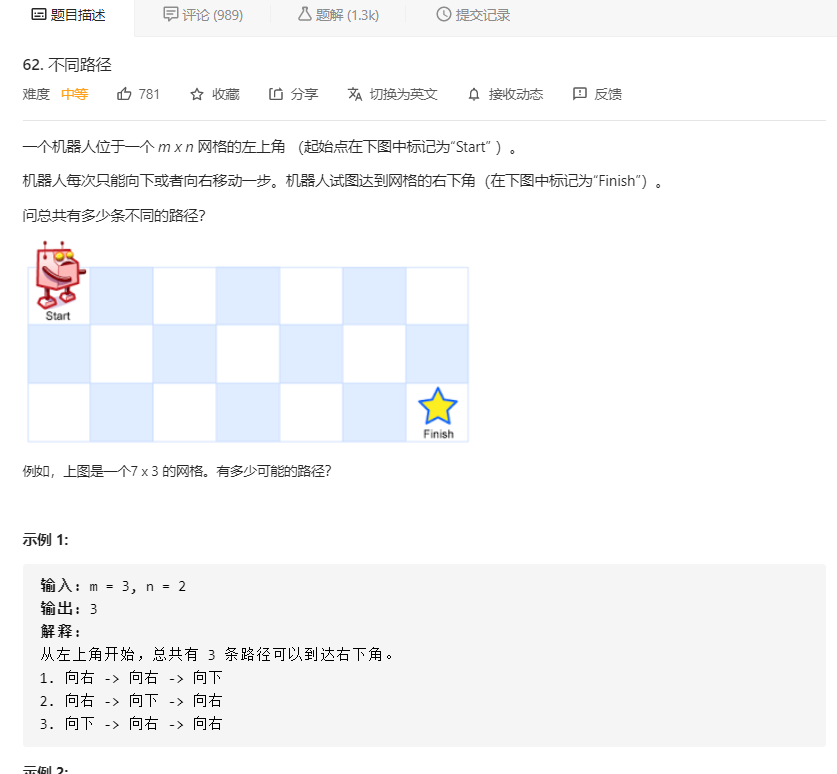
我们用 f(i, j)表示从左上角走到 (i, j) 的路径数量,其中 i 和 j 的范围分别是 [0, m)和 [0, n)。
由于我们每一步只能从向下或者向右移动一步,因此要想走到 (i, j),如果向下走一步,那么会从 (i−1,j) 走过来;
如果向右走一步,那么会从 (i, j-1)走过来。因此我们可以写出动态规划转移方程:
f(i, j) = f(i-1, j) + f(i, j-1)
需要注意的是,如果 i=0,那么 f(i-1,j)并不是一个满足要求的状态,我们需要忽略这一项;同理,如果 j=0,那么
f(i,j-1) 并不是一个满足要求的状态,我们需要忽略这一项。
初始条件为 f(0,0)=1,即从左上角走到左上角有一种方法。
最终的答案即为 f(m-1,n-1)。
代码实现如下:
public int uniquePaths(int m, int n) {
int[][] tmpResult=new int[m][n];
for(int i=0;i<n;i++){
tmpResult[0][i]=1;
}
for(int i=0;i<m;i++){
tmpResult[i][0]=1;
}
for(int i=1;i<m;i++){
for(int j=1;j<n;j++){
tmpResult[i][j] = tmpResult[i - 1][j] + tmpResult[i][j - 1];
}
}
return tmpResult[m-1][n-1];
}
方法二: 递归
递归则是从“Finish”出发,往上走,假设往上的位置是i,往左的位置是j,则有:
1.i>1且j>1 则有两条路线,继续往上找就好
2.i>1 或 j>1 则说明到了边缘,只有一种路线了,返回1就可以
3.i=1且j=1 说明是终点了,无路线了,返回0即可
代码实现如下:
public int uniquePaths(int m, int n) {
if(m==1 && n==1){
return 1;
}
return bianli(m,n);
}
public int bianli(int m, int n){
if(m>1 && n>1){
return bianli(m-1,n)+bianli(m,n-1);
}else if(n>1 || m>1){
return 1;
}else {
return 0;
}
}
虽然递归运算的结果和动态规划的结果相同,但是递归的在执行的时候却超时了,了解了一下,记录下
原因:
大家都知道递归的实现是通过调用函数本身,函数调用的时候,每次调用时要做地址保存,参数传递等,这是通过
一个递归工作栈实现的。具体是每次调用函数本身要保存的内容包括:局部变量、形参、调用函数地址、返回值。
那么,如果递归调用N次,就要分配N局部变量、N形参、N调用函数地址、N返回值,这势必是影响效率的,同时,
这也是内存溢出的原因,因为积累了大量的中间变量无法释放。
1.1用循环效率会比递归效率高吗?
递归与循环是两种不同的解决问题的典型思路。当然也并不是说循环效率就一定比递归高,递归和循环是两码事,
递归带有栈操作,循环则不一定,两个概念不是一个层次,不同场景做不同的尝试。
2.1递归算法:
优点:代码简洁、清晰,并且容易验证正确性。(如果你真的理解了算法的话,否则你更晕)
缺点:它的运行需要较多次数的函数调用,如果调用层数比较深,需要增加额外的堆栈处理(还有可能出现堆栈溢
出的情况),比如参数传递需要压栈等操作,会对执行效率有一定影响。但是,对于某些问题,如果不使用递归,
那将是极端难看的代码。
2.2循环算法:
优点:速度快,结构简单。
缺点:并不能解决所有的问题。有的问题适合使用递归而不是循环。如果使用循环并不困难的话,最好使用循环。
2.3递归算法和循环算法总结:
1) 一般递归调用可以处理的算法,也可以通过循环去解决,常需要额外的低效处理。
2)现在的编译器在优化后,对于多次调用的函数处理会有非常好的效率优化,效率未必低于循环。
3) 递归和循环两者完全可以互换。如果用到递归的地方可以很方便使用循环替换,而不影响程序的阅读,那么替
换成循环往往是好的。(例如:求阶乘的递归实现与循环实现。)