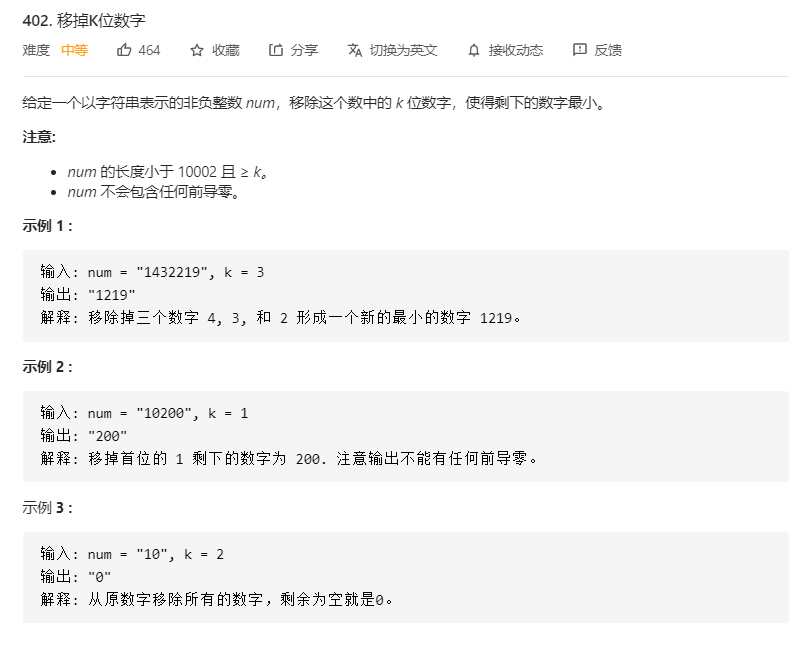
项目描述如下:
思路:
我自己想的是使用贪心算法
对于两个相同长度的数字序列,最左边不同的数字决定了这两个数字的大小,例如,对于 A = 1axxxA=1axxx,B = 1bxxxB=1bxxx,
如果 a > ba>b 则 A > BA>B。
基于此,我们可以知道,若要使得剩下的数字最小,需要保证靠前的数字尽可能小。

基于此我的代码实现如下:
public String removeKdigits(String num, int k) {
LinkedList<Character> tmp=new LinkedList<>();
int i=0;
//构建临时结果列表
for(;i<num.length()-k;i++){
tmp.add(num.charAt(i));
}
for(;i<num.length();i++){
tmp.add(num.charAt(i));
//删除一个数字
removeBig(tmp);
}
StringBuilder result=new StringBuilder();
for(Character charTmp:tmp){
if(charTmp=='0' && result.length()==0){
continue;
}
result.append(charTmp);
}
return result.length()==0?"0":result.toString();
}
public void removeBig(LinkedList<Character> tmp){
char prev=' ';
int index=-1;
for(Character charTmp:tmp){
if(prev!=' '&& prev>charTmp){
break;
}
prev=charTmp;
index++;
}
tmp.remove(index);
}
然而暴力的实现复杂度最差会达到 O(nk)(考虑整个数字序列是单调不降的),因此我们需要加速这个过程。
考虑从左往右增量的构造最后的答案。我们可以用一个栈维护当前的答案序列,栈中的元素代表截止到当前位置,
删除不超过 k 次个数字后,所能得到的最小整数。根据之前的讨论:在使用 k 个删除次数之前,栈中的序列从
栈底到栈顶单调不降。
因此,对于每个数字,如果该数字小于栈顶元素,我们就不断地弹出栈顶元素,直到
栈为空
或者新的栈顶元素不大于当前数字
或者我们已经删除了 k位数字
上述步骤结束后我们还需要针对一些情况做额外的处理:
如果我们删除了 mm 个数字且 m<km<k,这种情况下我们需要从序列尾部删除额外的 k-mk−m 个数字。
如果最终的数字序列存在前导零,我们要删去前导零。
如果最终数字序列为空,我们应该返回 00。
最终,从栈底到栈顶的答案序列即为最小数。
考虑到栈的特点是后进先出,如果通过栈实现,则需要将栈内元素依次弹出然后进行翻转才能得到最小数。为了避
免翻转操作,可以使用双端队列代替栈的实现。
代码实现如下:
public String removeKdigits(String num, int k) {
Deque<Character> queue=new LinkedList<>();
//我们假设num是一个递减的队列
for(int i=0;i<num.length();i++){
char tmpChar=num.charAt(i);
while (!queue.isEmpty() && k>0 && tmpChar<queue.peekLast()){
queue.pollLast();
k--;
}
queue.offerLast(tmpChar);
}
//处理单调递增的队列
for (int i=0;i<k;i++){
queue.pollLast();
}
StringBuilder result=new StringBuilder();
while (!queue.isEmpty()){
char charTmp=queue.pollFirst();
if(charTmp=='0' && result.length()==0){
continue;
}
result.append(charTmp);
}
return result.length()==0?"0":result.toString();
}