【noip模拟赛 王强的疑惑】 题解

考试题。

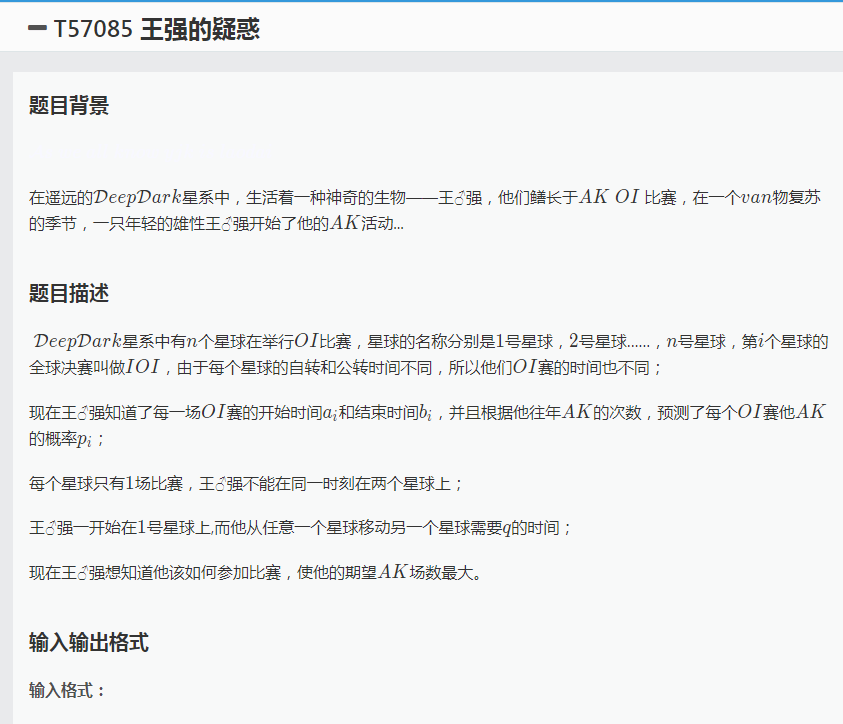
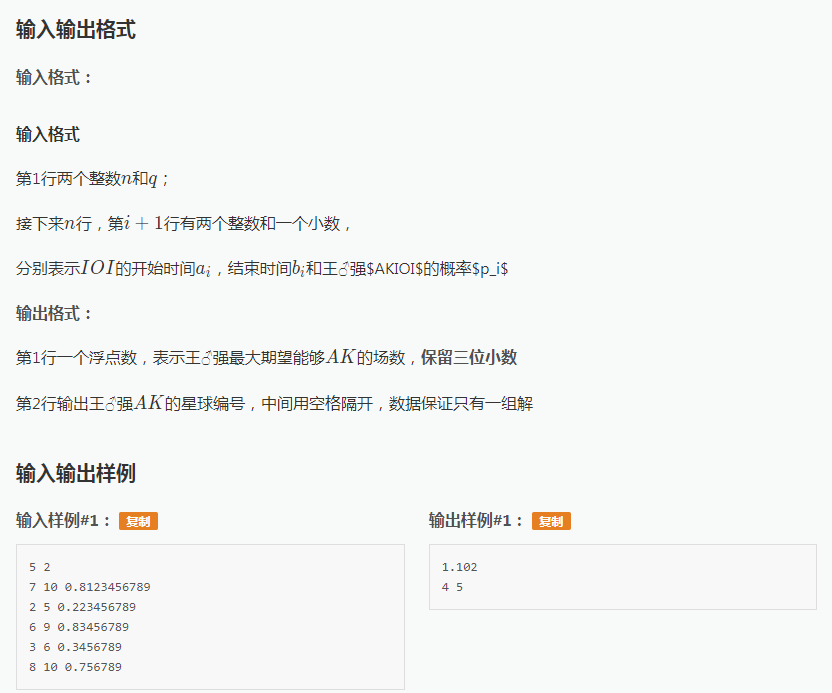
是个DP。

50分可以通过子集枚举+线段覆盖（贪心）完成。

考试没时间写了一个子集枚举30分。

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 20;
int read() {
    char ch = getchar(); int u = 0, f = 1;
    while (!isdigit(ch)) {if (ch == '-')f = -1; ch = getchar();}
    while (isdigit(ch)) {u = u * 10 + ch - 48; ch = getchar();}return u * f;
}
//int dp[maxn][maxn]...
struct ioi{
	int l, r, num;
	double p;
}b[maxn];
bool cmp(ioi a, ioi b)
{
	if(a.l == b.l) return a.r < b.r;
	return a.l < b.l;
}
int a[maxn], n, q, seq[maxn], last;
double now = 0, ans;
void print_subset(int s, int n)
{
	memset(a, 0, sizeof(a));
	for(int i = 1; i <= n; i++)
	if(s & (1 << (i-1))) a[i] = 1;
}
int main()
{
	freopen("math.in","r",stdin);
	freopen("math.out","w",stdout);
	n = read(); q = read();
	for(int i = 1; i <= n; i++)
	{
		b[i].l = read(); b[i].r = read(); scanf("%lf",&b[i].p);
		//cin>>b[i].l>>b[i].r>>b[i].p;
		b[i].r += q; b[i].num = i;
	}
	sort(b+1, b+1+n, cmp);
	for(int i = 1; i < (1 << n); i++)
	{
		print_subset(i, n);
		now = 0; last = 0;
		for(int j = 1; j <= n; j++)
		{
			if(a[j] == 1 && b[last].r <= b[j].l)
			{
				now += b[j].p;
				last = j;
			}
		}
		if(now > ans)
		{
			for(int j = 1; j <= n; j++)
			seq[j] = a[j];
			ans = now;
		}
	}
	printf("%0.3lf
",ans);
	for(int i = 1; i <= n; i++)
	{
		if(seq[i] == 1)
		printf("%d ", b[i].num);
	}
	return 0;
}

注意一点：memset初始化是O(n)的。尽管上次morslin跟我说做试验memset确实比for一遍快...所以我信了他每次枚举memset了一个1e6的数组..TLE

考虑正解的DP。

说过状态设的好，转移就方便。

一开始设的DP[i][j]表示前i个选了j个的最优..

转移个锤子。

正解：不妨设DP[i]表示在第i时，可以获得的最大期望（此期望非彼期望）。

于是只有在第j个结束时间为i才转移，其他的是DP[i] = DP[i-1]

注意a[j].l这个边界，要>q才能转移，会被卡。不写只有50分。

$ if(a[j].r == i && a[j].l >= q) $

$ DP[i] = max(DP[i], DP[a[j].l-q] + a[j].p) $

这时候得到一个O(MN)的DP。M为最大时间

考虑再优化，如果我们先给每个信息排一遍序，这样我们随着时间i的增大，每个a[j].l和a[j].r也在增大。记录上次枚举到的j是多少，记为pos，下次直接从j = pos开始。

我们再去枚举每个j的时候就不需要从1开始了，因为每次满足的先行条件是a[j].r == i。

注意一点，不论这次a[j]有没有更新DP[i]的值，我们的pos都要改变，否则还是TLE。

code：

#include <stack>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1e6 + 10;
inline int read() {
    char ch = getchar(); int u = 0, f = 1;
    while (!isdigit(ch)) {if (ch == '-')f = -1; ch = getchar();}
    while (isdigit(ch)) {u = u * 10 + ch - 48; ch = getchar();}return u * f;
}
double dp[maxn];
struct ioi{
	int l, r, num;
	double p;
}a[maxn];
int n, m, q, pos = 1, pre[maxn], ans[maxn], Ans[maxn], cnt;
bool cmp(ioi a, ioi b)
{
	if(a.r != b.r)
	return a.r < b.r;
	else return a.l < b.l;
}
int main()
{
	//freopen("math.in","r",stdin);
	//freopen("math.out","w",stdout);
	scanf("%d%d",&n,&q);
	for(int i = 1; i <= n; i++)
	{
		scanf("%d%d%lf",&a[i].l,&a[i].r,&a[i].p);
		a[i].num = i;
		m = max(m, a[i].r);
	}
	sort(a+1, a+1+n, cmp);
	
	for(int i = 1; i <= m; i++)
	{
 		dp[i] = dp[i-1]; pre[i] = i - 1;
		for(int j = pos; j <= n; j++)
		{
			if(a[j].r > i) break;
			if(a[j].r == i)
			{
				if(a[j].l >= q && dp[i] < dp[a[j].l-q] + a[j].p)
				{
					dp[i] = dp[a[j].l-q] + a[j].p;
					ans[i] = a[j].num;
					pre[i] = a[j].l - q;
				}
				if(a[j].num == 1 && dp[i] < dp[a[j].l-q] + a[j].p)
				{
					dp[i] = dp[a[j].l-q] + a[j].p;
					ans[i] = a[j].num;
					pre[i] = 0;
				}
				pos = j;
			}
		}
	}
	int now = m;
	while(now)
	{
		if(ans[now]) Ans[++cnt] = ans[now];
		now = pre[now];
	}
	printf("%0.3lf
",dp[m]);
	for(int i = cnt; i >= 1; i--)
	printf("%d ",Ans[i]);
	return 0;
}

输出路径的时候是while(now)，不是while(pre[now])..

我说怎么输出不了最后一个..