一.什么是莫队算法?
莫队算法是用来处理一类无修改的离线区间询问问题。——(摘自前国家队队长莫涛在知乎上对莫队算法的解释。)
莫队算法是前国家队队长莫涛在比赛的时候想出来的算法。
传说中能解决一切区间处理问题的莫队算法。
准确的说,是离线区间问题。但是现在的莫队被拓展到了有树上莫队,带修莫队(即带修改的莫队)。这里只先讲普通的莫队。

还有一点,重要的事情说三遍!莫队不是提莫队长!莫队不是提莫队长!!莫队不是提莫队长!!!
二.为什么要使用莫队算法?
看一个例题:给定一个n(n<50000)元素序列,有m(m<200000)个离线查询。每次查询一个区间L~R,问每个元素出现次数为k的有几个。(必须恰好是k,不能大于也不能小于)
这时候dalao们就直接树状数组线段树主席树拍上去了,身为蒟蒻的我躲在角落瑟瑟发抖。该怎么办?
这时候就要使用莫队算法了。
三.莫队算法的思想?
接着上面的例题,直接暴力怎么样??
肯定会T的啊。
但是如果这个暴力我们给优化一下呢?
我们想,有两个指针 curL 和 curR,curL 指向 L ,curR 指向 R。
L和R是一个区间的左右两端点。
利用 cnt[] 记录每个数出现的次数,每次只是 cnt[a[curL]] cnt[a[curR]] 修改。
举个栗子:

我们现在处理了curL—curR区间内的数据,现在左右移动,比如curL到curL-1,只需要更新上一个新的3,即curL-1。
那么curL到curL+1,我们只需要去除掉当前curL的值。因为curL+1是已经维护好了的。
curR同理,但是要注意方向哦!curR到curR+1是更新,curR到cur-1是去除。
我们先计算一个区间[curL curR]的answer,这样的话,我们就可以用O(1)转移到[curL-1 curR] [curL+1 curR] [curL curR+1] [curL curR-1]上来并且求出这些区间的answer。
我们利用curL和curR,就可以移动到我们所需要求的[L R]上啦~
这样做好像不会快很多,而且......
如果有个**数据,让你在每个L和R间来回跑,而且跨度很大呢??
该(T)还是(T)...
怎么办?
但是这其实就是莫队算法的核心了。我们的莫队算法还有优化。
这就是莫队算法最精明的地方(我认为的qwq),也正是有了这个优化,莫队算法被称为:优雅的暴力。
我们想,因为每次查询是离线的,所以我们先给每次的查询排一个序。
一种直观的办法是按照左端点排序,再按照右端点排序。但是这样的表现不好。特别是面对精心设计的数据,这样方法表现得很差。
举个栗子,有6个询问如下:(1, 100), (2, 2), (3, 99), (4, 4), (5, 102), (6, 7)。
这个数据已经按照左端点排序了。用上述方法处理时,左端点会移动6次,右端点会移动移动98+97+95+98+95=483次。
其实我们稍微改变一下询问处理的顺序就能做得更好:(2, 2), (4, 4), (6, 7), (5, 102), (3, 99), (1, 100)。
左端点移动次数为2+2+1+2+2=9次,比原来稍多。右端点移动次数为2+3+95+3+1=104,右端点的移动次数大大降低了。
上面的过程启发我们:
我们不应该严格按照升序排序,而是根据需要灵活一点的排序方法
那么排序的方法是
分块。
我们把所有的元素分成多个块。再按照左端点块编号从小到大排序,左端点块编号相同按右端点块编号从小到大。
这样对于不同的查询
例如:
我们有长度为9的序列。
1 2 3 4 5 6 7 8 9 分为1——3 4——6 7——9
查询有7组。[1 2] [2 9] [1 3] [6 9] [5 8] [3 8] [8 9]
排序后就是:[1 2] [1 3] [3 8] [2 9] | [5 8] [6 9] | [8 9]
然后我们按照这个顺序移动指针就好啦~
时间复杂度证明
其实从不同的角度看,证法很多:对于左端点在一个块中时,右端点最坏情况是从尽量左到尽量右,所以右端点跳时间复杂度O(n),左端点一共可以在n0.5个块中,所以总时间复杂度O(n*n0.5) = O(n^1.5)。
四.具体代码实现:
1.对于每组查询的记录和排序:
l,r为左右区间编号,p是第几组查询的编号
struct query{
int l, r, p;
}e[maxn];
bool cmp(query a, query b)
{
return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l < b.l;
}
2.处理和初始变量:
answer就是所求答案,bl是分块数量,a[]是原序列,ans[]是记录原查询序列下的答案,cnt[]是记录对于每个数i,cnt[i]表示i出现过的次数,curL和curR不再解释,nmk题意要求。
int answer, a[maxn], m, n, bl, ans[maxn], cnt[maxn], k, curL = 1, curR = 0;
void add(int pos)//添加
{
//do sth...
}
void remove(int pos)//去除
{
//do sth...
}
//一般写法都是边处理 边根据处理求答案。cnt[a[pos]]就是在pos位置上原序列a出现的次数。
3.主体部分及输出:
预处理查询编号,用四个while移动指针顺便处理。
n = read(); m = read(); k = read();
bl = sqrt(n);
for(int i = 1; i <= n; i++)
a[i] = read();
for(int i = 1; i <= m; i++)
{
e[i].l = read(); e[i].r = read();
e[i].p = i;
}
sort(e+1,e+1+m,cmp);
for(int i = 1; i <= m; i++)
{
int L = e[i].l, R = e[i].r;
while(curL < L)
remove(curL++);
while(curL > L)
add(--curL);
while(curR > R)
remove(curR--);
while(curR < R)
add(++curR);
ans[e[i].p] = answer;
}
for(int i = 1; i <= m; i++)
printf("%d
",ans[i]);
return 0;
在这里着重说下四个while
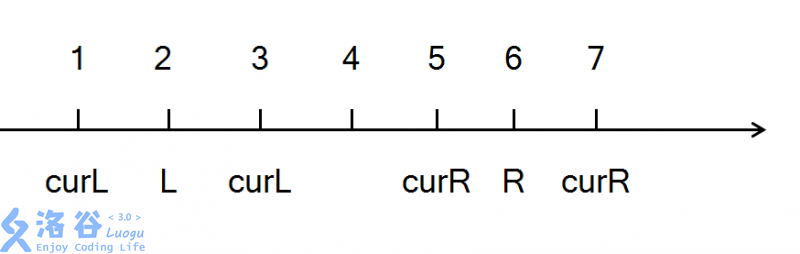
当curL < L 时,我们当前curL是已经处理好的了。所以remove时先去除当前curL再++
当curL > L 时,我们当前curL是已经处理好的了。所以 add 时先--再加上改后curL
当curR > R 时,我们当前curR是已经处理好的了。所以remove时先去除当前curR再--
当curR < R 时,我们当前curR是已经处理好的了。所以 add 时先++再加上改后curR
五.一些例题
【luogu P2709 小B的询问】
(add)和(remove)对于平方相加减的运算利用完全平方式逆回去。
1^2 = 1;
2^2 = (1+1)^2 = 1 + 1*2 + 1;
3^2 = (1+2)^2 = 1 + 2*2 + 4;
4^2 = (1+3)^2 = 1 + 3*2 + 9;
//小B的询问
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cmath>
using namespace std;
const int maxn = 50001;
int answer, a[maxn], m, n, bl, ans[maxn], cnt[maxn], k, curL = 1, curR = 0;
void add(int pos)
{
answer+=(((cnt[a[pos]]++)<<1)+1);//完全平方式展开
}
void remove(int pos)
{
answer-=(((--cnt[a[pos]])<<1)+1);//完全平方式展开
}
inline int read()
{
int k=0;
char c;
c=getchar();
while(!isdigit(c))c=getchar();
while(isdigit(c)){k=(k<<3)+(k<<1)+c-'0';c=getchar();}
return k;
}
struct query{
int l, r, p;
}e[maxn];
bool cmp(query a, query b)
{
return (a.l/bl) == (b.l/bl) ? a.r < b.r : a.l < b.l;
}
int main()
{
n = read(); m = read(); k = read();
bl = sqrt(n);
for(int i = 1; i <= n; i++)
a[i] = read();
for(int i = 1; i <= m; i++)
{
e[i].l = read(); e[i].r = read();
e[i].p = i;
}
sort(e+1,e+1+m,cmp);
for(int i = 1; i <= m; i++)
{
int L = e[i].l, R = e[i].r;
while(curL < L)
remove(curL++);
while(curL > L)
add(--curL);
while(curR > R)
remove(curR--);
while(curR < R)
add(++curR);
ans[e[i].p] = answer;
}
for(int i = 1; i <= m; i++)
printf("%d
",ans[i]);
return 0;
}
【luogu P4462 [CQOI2018]异或序列】
ax+ax-1+...+ay = cntx+cnty 这样把一段序列变成两段相加跑莫队。
#include <cstdio>
#include <algorithm>
#include <iostream>
#include <cmath>
using namespace std;
const int maxn = 200010;
int curR = 0, curL = 1, answer,a[maxn], ans[maxn], cnt[maxn], n, m, k, bl;
struct query{
int l,r,p;
}q[maxn];
bool cmp(const query &a, const query &b)
{
return (a.l/bl) == (b.l/bl) ? a.r<b.r : a.l<b.l;
}
inline void add(int pos)
{
cnt[a[pos]]++;
answer+=cnt[a[pos]^k];
}
inline void remove(int pos)
{
cnt[a[pos]]--;
answer-=cnt[a[pos]^k];
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
bl = sqrt(n);
cnt[0] = 1;
for(int i = 1; i <= n; i++)
{
scanf("%d",&a[i]);
a[i] ^= a[i-1];
}
for(int i = 1; i <= m; i++)
{
scanf("%d%d",&q[i].l,&q[i].r);
q[i].p = i;
}
sort(q+1,q+1+m,cmp);
for(int i = 1; i <= m; i++)
{
while(curL < q[i].l) remove(curL-1),curL++;
while(curL > q[i].l) curL--,add(curL-1);
while(curR < q[i].r) add(++curR);
while(curR > q[i].r) remove(curR--);
ans[q[i].p] = answer;
}
for(int i = 1; i <= m; i++)
printf("%d
",ans[i]);
return 0;
}
六.总结
莫队算法适用条件是比较苛刻的吗?是的。
①题目必须离线
②能够以极少的时间推出旁边区间(一般是O(1))
③没有修改或者修改不太苛刻
④基于分块,分块不行,它也好不了哪里去
但莫队的思想美妙,代码优美,你值得拥有。莫队的排序思想也为众多离线处理的题目提供了完整的思路。
我们可以看出来,对于莫队这种模拟式的暴力算法很好理解。
也比较实用,乱搞神器不是浪得虚名。
莫队是我自学的,所以在文章里或许会有些个人理解上的偏差,还请各位dalao能赐教。自学能力是需要培养、锻炼的。
其次是也引用了一些dalao写的很好的文章,也是我自学时用到的资料:
这是几篇我学莫队时参考的博客,如果觉得我讲的不够详细,可以借鉴。
祝各位OI路途能越走越顺!
本蒟蒻(QQ) 935145183/3203600070