1.符号表
符号表API:
| public class ST<Key,Value> | |
| ST() | 创建一张符号表 |
| void put(Key key,Value value) | 将键值对存入表中(若值为空则将键key从表中删除) |
| Value get(Key key) | 获取键key对应的值(若键key不存在则返回null) |
| void delete(Key key) | 从表中删去键key(及其对应的值) |
| boolean contains(Key key) | 键key在表中是否有对应的值 |
| boolean isEmpty() | 表是否为空 |
| int size() | 表中的键值对数量 |
| Iterable<Key> keys() | 表中的所有键的集合 |
1)泛型
2)重复的键:我们的所有实现都遵循以下规则:
a.每个键只对应一个值(表中不允许存在重复的键);
b.当用例代码向表中存入的键值对和表中已有的键(及相关联的值)冲突时,新的值会替代旧的值。
3)空(null)键:键不能为空。
4)空(null)值:我们还规定不允许有空值。我们可以将空值作为put()方法的第二个参数存入表中来实现删除。
5)删除:在符号表中,删除的实现可以有两种方法:延时删除,也就是将键对应的值置为空,然后在某个时候删去所有值为空的键;或是即时删除,也就是立刻从表中删除指定的键。刚才已经说过,put(key,null)是delete的一种简单的(延时型)实现。而实现(即时型)delete()就是为了替代这种默认的方案。在我们的符号表实现中不会使用默认的方案。
6)便捷方法
void delete(Key key){ put(key,null); } boolean contains(Key key){ return get(key)!=null; } boolean isEmpty(){ return size()==0; }
7)迭代
8)键的等价性。自定义的键需要重写equals()方法,最好使用不可变的数据类型作为键,否则表的一致性是无法保证的。
无序链表中的顺序查找
public class SequentialSearchST<Key, Value> { private Node first; private int N = 0; private class Node { Key key; Value val; Node next; public Node(Key key, Value val, Node next) { this.key = key; this.val = val; this.next = next; } } public Value get(Key key) { for (Node x = first; x != null; x = x.next) { if (key.equals(x.key)) { return x.val; } } return null; } public void put(Key key, Value val) { for (Node x = first; x != null; x = x.next) { if (key.equals(x.key)) { x.val = val; return; } } first = new Node(key, val, first); N++; } // Exercise 3.1.5 public int size() { return N; } public void delete(Key key) { first = delete(first, key); } private Node delete(Node x, Key key) { if (x == null) { return null; } if (x.key.equals(key)) { N--; return x.next; } x.next = delete(x.next, key); return x; } public Iterable<Key> keys() { Queue<Key> queue = new Queue<>(); for (Node x = first; x != null; x = x.next) { queue.enqueue(x.key); } return queue; } }
有序数组中的二分查找
public class BinarySearchST<Key extends Comparable<Key>, Value> { private Key[] keys; private Value[] vals; private int N; public BinarySearchST(int capacity) { keys = (Key[]) new Comparable[capacity]; vals = (Value[]) new Object[capacity]; } public int size() { return N; } public Value get(Key key) { if (isEmpty()) { return null; } int i = rank(key); if (i < N && keys[i].compareTo(key) == 0) { return vals[i]; } else { return null; } } public boolean isEmpty() { return N == 0; } public int rank(Key key) { int lo = 0, hi = N - 1; while (lo <= hi) { int mid = lo + (hi - lo) / 2; int cmp = key.compareTo(keys[mid]); if (cmp < 0) { hi = mid - 1; } else if (cmp > 0) { lo = mid + 1; } else { return mid; } } return lo; } public void put(Key key, Value val) { int i = rank(key); if (i < N && keys[i].compareTo(key) == 0) { vals[i] = val; return; } for (int j = N; j > i; j--) { keys[j] = keys[j - 1]; vals[j] = vals[j - 1]; } keys[i] = key; vals[i] = val; N++; assert check(); } /** * Exercise 3.1.16 * * @param key */ public void delete(Key key) { if (isEmpty()) { return; } int i = rank(key); if (i < N && keys[i].compareTo(key) == 0) { for (int j = i; j < N - 1; j++) { keys[j] = keys[j + 1]; vals[j] = vals[j + 1]; } N--; keys[N] = null; vals[N] = null; } assert check(); } public Key min() { return keys[0]; } public Key max() { return keys[N - 1]; } public Key select(int k) { return keys[k]; } public Key ceiling(Key key) { int i = rank(key); return keys[i]; } /** * Exercise 3.1.17 * * @param key * @return */ public Key floor(Key key) { int i = rank(key); if (i < N) { if (keys[i].compareTo(key) == 0) { return key; } else if (i > 0) { return keys[i - 1]; } } return null; } public Iterable<Key> keys(Key lo, Key hi) { Queue<Key> q = new Queue<Key>(); for (int i = rank(lo); i < rank(hi); i++) { q.enqueue(keys[i]); } if (contains(hi)) { q.enqueue(keys[rank(hi)]); } return q; } public boolean contains(Key key) { return get(key) != null; } // Add for Exercise 3.1.29 public Iterable<Key> keys() { return keys(min(), max()); } public void deleteMin() { delete(min()); } public void deleteMax() { delete(max()); } // Exercise 3.1.30 private boolean check() { return isSorted() && rankCheck(); } private boolean isSorted() { for (int i = 1; i < size(); i++) { if (keys[i].compareTo(keys[i - 1]) < 0) { return false; } } return true; } private boolean rankCheck() { for (int i = 0; i < size(); i++) { if (i != rank(select(i))) { return false; } } for (int i = 0; i < size(); i++) { if (keys[i].compareTo(select(rank(keys[i]))) != 0) { return false; } } return true; } }
2.二叉查找树
1)数据表示
和链表一样,我们嵌套定义了一个私有类来表示二叉查找树上的一个结点。每个结点都含有一个键,一个值,一条左链接,一条右链接和一个结点计数器。私有方法size()会将空链接的值当作0,这样我们就能保证以下公式对于二叉树中的任意结点x总是成立。
size(x)=size(x.left)+size(x.right)+1;
2)查找
一般来说,在符号表中查找一个键可能得到两种结果。如果含有该键的结点存在于表中,我们的查找就命中了,然后返回相应的值。否则查找未命中(并返回null)。
根据数据表示的递归结构我们马上就能得到,在二叉查找树中查找一个键的递归算法:如果树是空的,则查找未命中;如果被查找的键和根结点的键想等,查找命中,否则我们就(递归地)在适当的子树中继续查找。
3)插入
当查找一个不存在于树中的结点并结束于一条空链接时,我们需要做的就是将链接指向一个含有被查找的键的新结点。
4)递归
可以将递归调用前的代码想象成沿着树向下走:它会将给定的键和每个结点的键相比较并根据向左或者向右移动到下一个结点。然后可以将递归调用后的代码想象成沿着树向上爬。
public class BST<Key extends Comparable<Key>, Value> { private Node root; private class Node { private Key key; private Value val; private Node left, right; private int N; public Node(Key key, Value val, int N) { this.key = key; this.val = val; this.N = N; } } public int size() { return size(root); } private int size(Node x) { if (x == null) { return 0; } else { return x.N; } } public Value get(Key key) { return get(root, key); } private Value get(Node x, Key key) { if (x == null) { return null; } int cmp = key.compareTo(x.key); if (cmp < 0) { return get(x.left, key); } else if (cmp > 0) { return get(x.right, key); } else { return x.val; } } public void put(Key key, Value val) { root = put(root, key, val); } private Node put(Node x, Key key, Value val) { if (x == null) { return new Node(key, val, 1); } int cmp = key.compareTo(x.key); if (cmp < 0) { x.left = put(x.left, key, val); } else if (cmp > 0) { x.right = put(x.right, key, val); } else { x.val = val; } x.N = size(x.left) + size(x.right) + 1; return x; }
有序性相关的方法与删除操作
1)最大键和最小键
如果根结点的左链接为空,那么一颗二叉查找树中最小的键就是根结点;如果左链接非空,那么树中的最小键就是左子树中的最小键。找出最大键的方法也是类似的,只是变为查找右子树而已。
public Key min() { return min(root).key; } private Node min(Node x) { if (x.left == null) { return x; } return min(x.left); } public Key max(){ return max(root).key; } private Node max(Node x){ if(x.right==null){ return x; } return max(x.right); }
2)向上取整和向下取整
如果给定的键key小于二叉查找树的根结点的键,那么小于等于key的最大键floor(key)一定在根结点的左子树中;如果给定的键key大于二叉查找树的根结点,那么只有当根结点右子树中存在小于等于key的结点时,小于等于key的最大键才会出现在右子树中,否则根结点就是小于等于key的最大键。将“左”变为“右”(同时将小于变为大于)就能够得到ceiling()的算法。
public Key floor(Key key) { Node x = floor(root, key); if (x == null) { return null; } return x.key; } private Node floor(Node x, Key key) { if (x == null) { return null; } int cmp = key.compareTo(x.key); if (cmp == 0) { return x; } if (cmp < 0) { return floor(x.left, key); } Node t = floor(x.right, key); if (t != null) { return t; } else { return x; } } public Key ceiling(Key key) { Node x = ceiling(root, key); if (x == null) { return null; } return x.key; } private Node ceiling(Node x, Key key) { if (x == null) { return null; } int cmp = key.compareTo(x.key); if (cmp == 0) { return x; } if (cmp > 0) { return floor(x.right, key); } Node t = floor(x.left, key); if (t != null) { return t; } else { return x; } }
3)选择操作
我们在二叉查找树的每个结点中维护的子树结点计数器变量N就是用来支持此操作的。
假设我们想找到排名为k的键(即树中正好有k个小于它的键)。如果左子树中的结点数t大于k,那么我们就继续(递归地)在左子树中查找排名为k的键;如果t等于k,我们就返回根结点中的键;如果t小于k,我们就(递归地)在右子树中查找排名为(k-t-1)的键。
4)排名
rank()是select()的逆方法,它会返回给定键的排名。它的实现和select()类似:如果给定的键和根结点的键相等,我们返回左子树中的结点总数t;如果给定的键小于根结点,我们会返回该键在左子树中的排名(递归计算);如果给定的键大于根结点,我们会返回t+1(根结点)加上它在右子树中的排名(递归计算)。
public Key select(int k) { return select(root, k).key; } private Node select(Node x, int k) { if (x == null) { return null; } int t = size(x.left); if (t > k) { return select(x.left, k); } else if (t < k) { return select(x.right, k - t - 1); } else { return x; } } public int rank(Key key) { return rank(key, root); } private int rank(Key key, Node x) { if (x == null) { return 0; } int cmp = key.compareTo(x.key); if (cmp < 0) { return rank(key, x.left); } else if (cmp > 0) { return 1 + size(x.left) + rank(key, x.right); } else { return size(x.left); } }
5)删除最大键和删除最小键
二叉查找树中最难实现的方法就是delete()方法,即从符号表删除一个键值对。作为热身运动,我们先考虑deleteMin()方法(删除最小键所对应的键值对)。
和put()一样,我们的递归方法接受一个指向结点的链接,并返回一个指向结点的链接。这样我们就能够方便地改变树的结构,将返回的链接赋给作为参数的链接。
对于deleteMin(),我们要不断深入根结点的左子树中直至遇见一个空链接,然后将指向该结点的链接指向该结点的右子树(只需要在递归调用中返回它的右链接即可)。此时已经没有任何链接指向要被删除的结点,因此它会被垃圾收集器清理掉。我们给出的标准递归代码在删除结点后会正确地设置它的父结点的链接并更新它到根结点的路径上的所有结点的计数器的值。deleteMax()方法的实现和deleteMin()完全类似。
public void deleteMin() { root = deleteMin(root); } private Node deleteMin(Node x) { if (x.left == null) { return x.right; } x.left = deleteMin(x.left); x.N = size(x.left) + size(x.right) + 1; return x; } public void deleteMax() { root = deleteMax(root); } private Node deleteMax(Node x) { if (x.right == null) { return x.left; } x.right = deleteMax(x.right); x.N = size(x.left) + size(x.right) + 1; return x; }
6)删除操作
我们可以用类似的方式删除任意只有一个子结点(或者没有子结点)的结点,但应该怎样删除一个拥有两个子结点的结点呢?删除之后我们要处理两颗子树,但被删除结点的父结点只有一条空出来的链接。
方法:在删除结点x后用它的后继结点填补它的位置。因为x有一个右子结点,因此它的后继结点就是其右子树中的最小结点。这样的替换仍然能够保证树的有序性,因为x.key和它的后继结点的键之间不存在其他的键。我们能够用4个简单的步骤完成将x替换为它的后继结点的任务:
1)将指向即将被删除的结点的链接保存为t;
2)将x指向它的后继结点min(t.right);
3)将x的右链接(原本指向一颗所有结点都大于x.key的二叉查找树)指向deleteMin(t.right),也就是在删除后所有结点仍然都大于x.key的子二叉查找树。
4)将x的左链接(本为空)设为t.left(其下所有的键都小于被删除的结点和它的后继结点)。
在递归调用后我们会修正被删除结点的父结点的链接,并将由此结点到根结点的路径上的所有结点的计数器减1(这里计数器的值仍然会被设为其所有子树中的结点总数加一)。尽管这种方法能够正确地删除一个结点,它的缺陷是可能会在某些实际应用中产生性能问题。这个问题在于选用后继结点是一个随意的决定,并没有考虑树的对称性。
public void delete(Key key) { root = delete(root, key); } private Node delete(Node x, Key key) { if (x == null) { return null; } int cmp = key.compareTo(x.key); if (cmp < 0) { x.left = delete(x.left, key); } else if (cmp > 0) { x.right = delete(x.right, key); } else { if (x.right == null) { return x.left; } if (x.left == null) { return x.right; } Node t = x; x = min(t.right); x.right = deleteMin(t.right); x.left = t.left; } x.N = size(x.left) + size(x.right) + 1; return x; }
7)范围查找
要实现能够返回给定范围内键的keys()方法,我们首先需要一个遍历二叉查找树的基本方法,叫做中序遍历。
private void print(Node x){ if(x==null) return; print(x.left); StdOut.println(x.key); print(x.right); }
为了实现接受两个参数并能够将给定范围内的键返回给用例的keys()方法,我们可以修改一下这段代码,将所有落在给定范围以内的键加入一个队列Queue并跳过那些不可能含有所查找键的子树。
public Iterable<Key> keys() { return keys(min(), max()); } public Iterable<Key> keys(Key lo, Key hi) { Queue<Key> queue = new Queue<Key>(); keys(root, queue, lo, hi); return queue; } private void keys(Node x, Queue<Key> queue, Key lo, Key hi) { if (x == null) { return; } int cmplo = lo.compareTo(x.key); int cmphi = hi.compareTo(x.key); if (cmplo < 0) { keys(x.left, queue, lo, hi); } if (cmplo <= 0 && cmphi >= 0) { queue.enqueue(x.key); } if (cmphi > 0) { keys(x.right, queue, lo, hi); } }
3.2-3查找树
为了保证查找树的平衡性,我们需要一些灵活性,因此在这里我们允许树中的一个结点保存多个键。确切地说,我们将一颗标准的二叉查找树中的结点称为2-结点(含有一个键和两条链接),而现在我们引入3-结点,它含有两个键和三条链接。2-结点和3-结点中的每条链接都对应着其中保存的键所分割产生的一个区间。
定义。一颗2-3查找树或为一颗空树,或由以下结点组成:
a.2-结点,含有一个键(及其对应的值)和两条链接,左链接指向的2-3树中的键都小于该结点,右链接指向的2-3树中的键都大于该结点。
b.3-结点,含有两个键(及其对应的值)和三条链接,左链接指向的2-3树的键都小于该结点,中链接指向的2-3树中的键都位于该结点的两个键之间,右链接指向的2-3树中的键都大于该结点。
一颗完美平衡的2-3查找树中的所有空链接到根结点的距离都应该是相同的。简洁起见,这里我们用2-3树指代一颗完美平衡的2-3查找树。
1)查找
将二叉查找树的查找算法一般化我们就能够直接得到2-3树的查找算法。要判断一个键是否在树中,我们先将它和根结点中的键比较。如果它和其中任意一个相等,查找命中;否则我们就根据比较的结果找到指向相应区间的链接,并在其指向的子树中递归地继续查找。如果这是个空链接,查找未命中。
2)向2-结点中插入新键
要在2-3树中插入一个新结点,我们可以和二叉查找树一样先进行一次未命中的查找,然后把新结点挂在树的底部。但这样的话树无法保持完美平衡性。我们使用2-3树的主要原因就在于它能够在插入后继续保持平衡。如果未命中的查找结束于一个2-结点,事情就好办了:我们只要把这个2-结点替换为一个3-结点,将要插入的键保存在其中即可。如果未命中的查找结束于一个3-结点,事情就要麻烦一些。
3)向一颗只含有一个3-结点的树中插入新键
在考虑一般情况之前,先假设我们需要向一颗只含有一个3-结点的树中插入一个新键。这棵树中有两个键,所以在它唯一的结点中已经没有可插入新键的空间了。为了将新键插入,我们先临时将新键存入该结点中,使之称为一个4-结点。它很自然地扩展了以前的结点并含有3个键和4个链接。创建一个4-结点很方便,因为很容易将它转换为一颗由3个2-结点组成的2-3树,其中一个结点(根)含有中键,一个结点含有3个键中的最小者(和根结点的左链接相连),一个结点含有3个键中的最大者(和根结点的右链接相连)。这棵树既是一颗含有3个结点的二叉查找树,同时也是一颗完美平衡的2-3树,因为其中所有的空链接到根结点的距离都相等。插入前树的高度为0,插入后树的高度为1。
4)向一个父结点为2-结点的3-结点中插入新键
作为第二轮热身,假设未命中的查找结束于一个3-结点,而它的父结点是一个2-结点。在这种情况下我们需要在维持树的完美平衡的前提下为新键腾出空间。我们先像刚才一样构造一个临时的4-结点并将其分解,但此时我们不会为中键创建一个新结点,而是将其移动至原来的父结点中。你可以将这次转换看成将指向原3-结点的一条链接替换为新父结点中的原中键左右两边的两条链接,并分别指向两个新的2-结点。
根据我们的假设,父结点是一个2-结点(一个键两条链接),插入之后变为了一个3-结点(两个键3条链接)。另外,这次转换也并不影响(完美平衡的)2-3树的主要性质。树仍然是有序的,因为中键被移动到父结点去了;树仍然是完美平衡的,插入后所有的空链接到根结点的距离仍然相同。
5)向一个父结点为3-结点的3-结点中插入新键
现在假设未命中的查找结束于一个父结点为3-结点的结点。我们再次和刚才一样构造一个临时的4-结点并分解它,然后将它的中键插入它的父结点中。但父结点也是一个3-结点,因此我们再用这个中键构造一个新的临时4-结点,然后在这个结点上进行相同的变换,即分解这个父结点并将它的中键插入到它的父结点中去。推广到一般情况,我们就这样一直向上不断分解临时的4-结点并将中键插入更高层的父结点,直至遇到一个2-结点并将它替换为一个不需要继续分解的3-结点,或者到达3-结点的根。
6)分解根结点
如果从插入结点到根结点的路径上全都是3-结点,我们的根结点最终变成一个临时的4-结点。此时我们可以按照向一颗只有3-结点的树中插入新键的方法处理这个问题。我们将临时的4-结点分解为3个2-结点,使得树高加1。这次最后的变换仍然保持了树的完美性,因为它变换的是根节点。
7)局部变换
将一个4-结点分解为一颗2-3树可能有6种情况。这4-结点可能是根结点,可能是一个2-结点的左子结点或者右子结点,有可能是一个3-结点的左子结点,中子结点或者右子结点。3-3树插入算法的根本在于这些变换都是局部的:除了相关的结点和链接之外不必修改后者检查树的其他部分。每次变换中,变更的链接数量不会超过一个很小的常数。需要特别指出的是,不光是在树的底部,树中的任何地方只要符合相应的模式,变换都可以进行。每个变换都会将4-结点中的一个键送入它的父结点中,并重构相应的链接不必涉及树的其他部分。
8)全局性质
这些局部变换不会影响树的全局有序性和平衡性:任意空链接到根结点的路径长度都是相等的。
和标准的二叉查找树由上向下生长不同,2-3树的生长是由下向上的。
2-3树的分析和二叉查找树的分析大不相同,因为我们主要感兴趣的是最坏情况下的性能,而非一般情况。
命题F。在一颗大小为N多2-3树中,查找和插入操作访问的结点必然不超过lgN个。
因此,我们可以确定2-3树在最坏情况下仍有较好的性能。每个操作中处理每个结点的时间都不会超过一个很小的常数,且这两个操作只会访问一条路径上的结点,所以任何查找或者插入的成本都肯定不会超过对数级别。
但是,我们和真正的实现还有一段距离。尽管我们可以用不同的数据类型表示2-结点和3-结点并写出变换所需的代码,但用这种直白的表示方法实现大多数的操作并不方便,因为需要处理的情况实在太多。我们需要维护两种不同类型的结点,将被查找的键和结点中的每个键进行比较,将链接和其他信息从一种结点复制到另一种结点,将结点从一种数据类型转换到另一种数据类型,等等。实现这些不仅需要大量的代码,而且它们所产生的额外开销可能会使算法比标准的二叉查找树更慢。平衡一棵树的初衷是为了消除最坏情况,但我们希望这种保障所需的代码能够越少越好。幸运的是,我们只需要一点点代价就能用一种统一的方式完成所有变换。
4.红黑二叉查找树
1)替换3-结点
红黑二叉查找树背后的基本思想是用标准的二叉查找树(完全由2-结点构成)和一些额外的信息(替换3-结点)来表示2-3树。
我们将树中的链接分为两种类型:红链接将两个2-结点连接起来构成一个3-结点,黑链接则是2-3树中的普通链接。确切的说,我们将3-结点表示为由一条左斜的红色链接(两个2-结点其中之一是另一个的左子结点)相连的两个2-结点。
这种表示法的一个优点是,我们无需修改就可以直接使用标准二叉查找树的get()方法。对于任意的2-3树,只要对结点进行转换,我们都可以立即派生出一颗对应的二叉查找树。我们将用这种方式表示2-3树的二叉查找树称为红黑二叉查找树。
2)一种等价的定义
红黑树的另一种定义是含有红黑链接并满足下列条件的二叉查找树:
a.红链接均为左链接;
b.没有任何一个结点同时和两条红链接相连;
c.该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链接数量相同。
3)一一对应
如果我们将一颗红黑树中的红链接画平,那么所有的空链接到根结点的距离都将是相同的。如果我们将由红链接相连的结点合并,得到的就是一颗2-3树。
相反,如果将一颗2-3树中的3-结点画作由红色左链接相连的两个2-结点,那么不会存在能够和两个红链接相连的结点,且树必然是完美黑色平衡的,因为黑链接即2-3树中的普通链接,根据定义这些链接必然是完美平衡的。
4)颜色表示
方便起见,因为每个结点都只会有一条指向自己的链接(从它的父结点指向它),我们将链接的颜色保存在表示结点的Node数据类型的布尔变量color中。如果指向它的链接是红色的,那么该变量为true,黑色则为false。我们约定空链接为黑色。为了代码的清晰我们定义了两个常量RED和BLACK来设置和测试这个变量。我们使用私有方法isRed()来测试一个结点和它的父结点之间的链接的颜色。当我们提到一个结点的颜色时,我们指的是指向该结点的链接的颜色,反之亦然。
private static final boolean RED = true; private static final boolean BLACK = false; private class Node { private Key key; private Value val; private Node left, right; private int N; private boolean color; public Node(Key key, Value val, int N, boolean color) { this.key = key; this.val = val; this.N = N; this.color = color; } } private boolean isRed(Node x) { if (x == null) { return false; } return x.color == RED; }

5)旋转
我们实现的某些操作中可能会出现红色右链接或者两条连续的红链接,但在操作完成前这些情况都会被小心地旋转并修复。旋转操作会改变红链接的指向。
首先,假设我们有一条红色的右链接需要被转化为左链接。这个操作叫做左旋转,它对应的方法接收一条指向红黑树中的某个结点的链接作为参数。假设被指向的结点的右链接是红色的,这个方法会对树进行必要的调整并返回一个指向包含同一组键的子树且其左链接为红色的根结点的链接。
private Node rotateLeft(Node h) { Node x = h.right; h.right = x.left; x.left = h; x.color = h.color; h.color = RED; x.N = h.N; h.N = 1 + size(h.left) + size(h.right); return x; }
这个操作很容易理解:我们只是将用两个键中较小的者作为根结点变为将较大者作为根结点。
实现将一个红色左链接转换为一个红色右链接的一个右旋转的代码完全相同,只需要将left和right互换即可。
private Node rotateRight(Node h) { Node x = h.left; h.left = x.right; x.right = h; x.color = h.color; h.color = RED; x.N = h.N; h.N = 1 + size(h.left) + size(h.right); return x; }

6)在旋转后重置父结点的链接
无论左旋转还是右旋转,旋转操作都会返回一条链接。我们总是会用rotateRight()或rotateLeft()的返回值重置父结点(或是根结点)中相应的链接。返回的链接可能是左链接也可能是右链接,但是我们总会将它赋予父结点中的链接。
这个链接可能是红色也可能是黑色---rotateLeft()和rotateRight()都通过将x.color设为h.color保留它原来的颜色。这可能会产生两条连续的红链接,但我们的算法会继续用旋转操作修正这种情况。例如,代码h=rotateLeft(h);将旋转结点h的红色右链接,使得h指向了旋转后的子树的根结点(组成该子树中的所有键和旋转前相同,只是根结点发生了变化)。这种简洁的代码是我们使用递归实现二叉查找树的各种方法的主要原因。你会看到,它使得旋转操作称为了普通插入操作的一个简单补充。
在插入新的键时我们可以使用旋转操作帮助我们保证2-3树和红黑树之间的一一对应关系,因为旋转操作可以保持红黑树的两个重要性质:有序性和完美平衡性。也就是说,我们在红黑树中进行旋转时无需为树的有序性或者完美平衡性担心。
下面我们来看看应该如何使用旋转操作来保持红黑树的另外两个重要性质(不存在两条连续的红链接和不存在红色的右链接)。
7)向单个2-结点中插入新键
一颗只含有一个键的红黑树只含有一个2-结点。插入另一个键之后,我们马上就需要将它们旋转。如果新键小于老键,我们只需要新增一个红色的结点即可,新的红黑树和单个3-结点完全等价。
如果新键大于老键,那么新增的红色结点将会产生一条红色的右链接。我们需要root=rotateLeft(root);来将其旋转为红色左链接并修正根结点的链接,插入操作才算完成。
两种情况的结果均为一颗和单个3-结点等价的红黑树,其中含有两个键,一条红链接,树的黑链接高度为1。

8)向树底部的2-结点插入新键
用和二叉查找树相同的方式向一颗红黑树中插入一个新键会在树的底部新增一个结点(为了保证有序性),但总是用红链接将新结点和它的父结点相连。如果它的父结点是一个2-结点,那么刚才讨论的两种处理方法仍然适用。如果指向新结点的是父结点的左链接,那么父结点就直接成为了一个3-结点;如果指向新结点的是父结点的右链接,这就是一个错误的3-结点,但一次左旋转就能够修复它。

9)向一颗双键树(即一个3-结点)中插入新键
这种情况又可分为三种子情况:新键小于树中的两个键,在两者之间,或是大于树中的两个键。每种情况中都会产生一个同时连接到两条红链接的结点,而我们的目标就是修正这一点。
a.三者中最简单的情况是新键大于原树中的两个键,因此它被链接到3-结点的右链接。此时,树是平衡的,根结点为中间大小的键,它有两条红链接分别和较小和较大的结点相连。如果我们将两条链接的颜色都由红变为黑,那么我们就得到了一颗由三个结点组成,高为2的平衡树。它正好能够对应一颗2-3树。其他两种情况最终也会转化为这种情况。
b.如果新键小于原树中的两个键,它会被连接到最左边的空链接,这样就产生了两条连续的红链接。此时我们只需要将上层的红链接右旋转即可得到第一种情况(中值键为根结点并和其他两个结点用红链接相连)。
c.如果新键介于原树中的两个键之间,这又会产生两条连续的红链接,一条红色左链接接一条红色右链接。此时我们只需要将下层的红链接左旋转即可得到第二种情况(两条连续的红色链接)。
总的来说,我们通过0次,1次和2次旋转以及颜色的变化得到了期望的结果。

10)颜色转换
我们专用一个方法flipColors()来转换一个结点的两个红色子结点的颜色。除了将子结点的颜色由红变黑之外,我们同时还要将父结点的颜色由黑变红。这项操作最重要的性质在于它和旋转操作一样是局部变换,不会影响整棵树的黑色平衡性。
private void flipColors(Node h) { h.color = !h.color; h.left.color = !h.left.color; h.right.color = !h.right.color; }
11)根结点总是黑色的
颜色转换会使根结点变为红色。这也可能出现在很大的红黑树中。严格地说,红色的根结点说明根结点是一个3-结点的一部分,但实际情况并不是这样。因此我们在每次插入后都会将根结点设为黑色。注意,每当根结点由红变黑时树的黑链接高度就会加1。
12)向树底部的3-结点插入新键
现在假设我们需要在树的底部的一个3-结点下加入一个新结点。前面讨论过的三种情况都会出现。指向新结点的链接可能是3-结点的右链接(此时我们只需要转换颜色即可),或是左链接(此时我们需要进行右旋转然后再转换颜色),或是中链接(此时我们需要先左旋转下层链接然后右旋转上层链接,最后再转换颜色)。颜色转换会使到中结点的链接变红,相当于将它送入了父结点。这意味着在父结点中继续插入一个新键,我们也会继续用相同的办法解决这个问题。
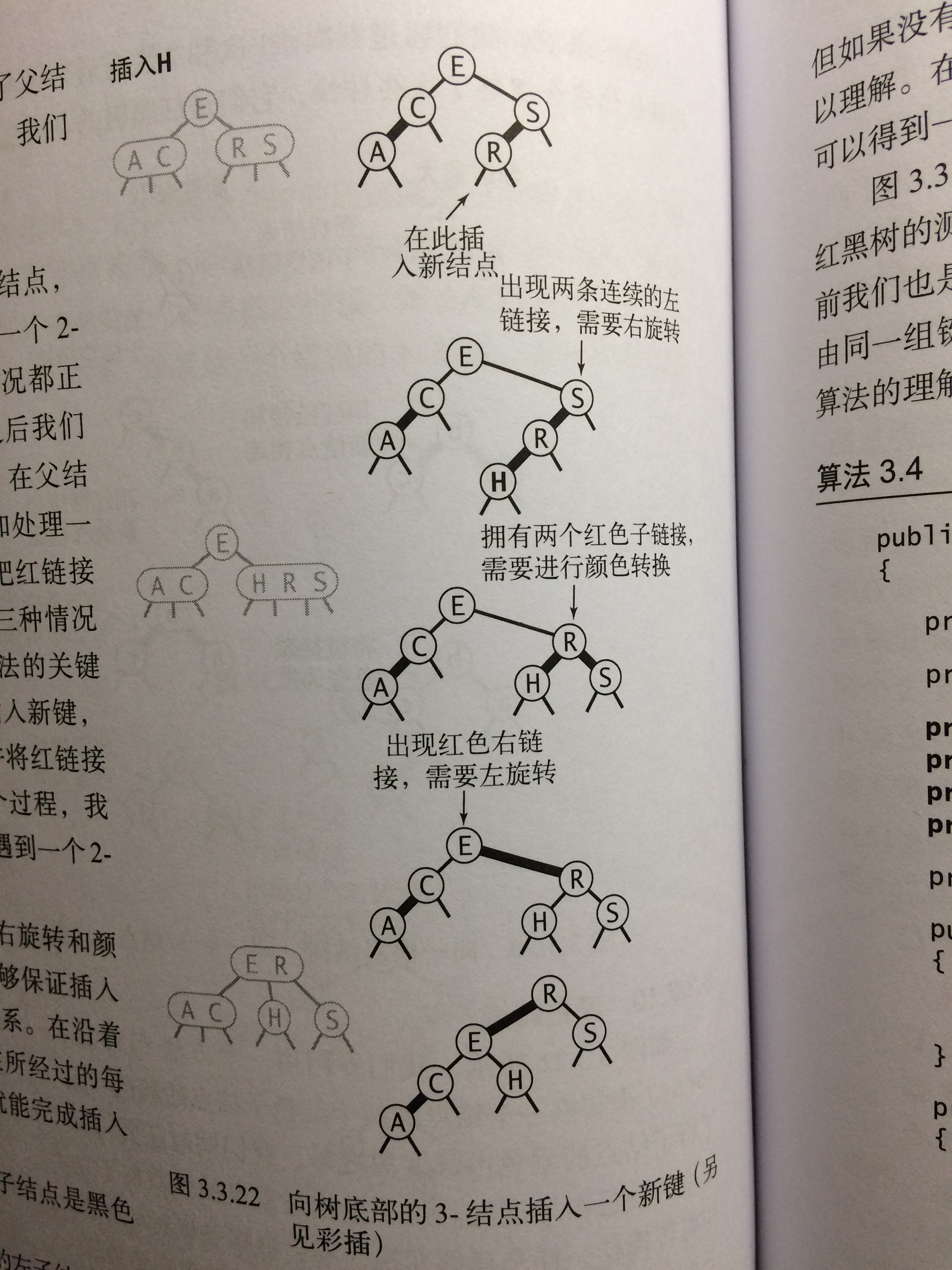
13)将红链接在树中向上传递
2-3树中的插入算法需要我们分解3-结点,将中间键插入父结点,如此这般直到遇到一个2-结点或是根结点。我们所考虑过的所有情况都正是为了达成这个目标:每次必要的旋转之后我们都会进行颜色转换,这使得中结点变红。在父结点看来,处理这样一个红色结点的方式和处理一个新插入的红色结点的方式和处理一个新插入的红色结点完全相同,即继续把红链接转移到中结点上去。
在红黑树中实现2-3树的插入算法的关键操作所需步骤:要在一个3-结点下插入新键,先创建一个临时的4-结点,将其分解并将红链接由中间键传递给它的父结点。重复这个过程,我们就能将红链接在树中向上传递,直至遇到一个2-结点或者根节点。
总之,只要谨慎地使用左旋转,右旋转和颜色转换这三种简单的操作,我们就能保证插入操作后红黑树和2-3树一一对应关系。在沿着插入点到根结点的路径向上移动时在所经过的每个结点中顺序完成以下操作,我们就能完成插入操作。
14)实现
因为保持树的平衡性所需的操作是由下向上在每个经过的结点中进行的,将它们植入我们已有的实现中十分简单:只需要在递归调用之后完成这些操作即可。
public void put(Key key, Value val) { root = put(root, key, val); root.color = BLACK; } private Node put(Node h, Key key, Value val) { if (h == null) { return new Node(key, val, 1, RED); } int cmp = key.compareTo(h.key); if (cmp < 0) { h.left = put(h.left, key, val); } else if (cmp > 0) { h.right = put(h.right, key, val); } else { h.val = val; } if (isRed(h.right) && !isRed(h.left)) { h = rotateLeft(h); } if (isRed(h.left) && isRed(h.left.left)) { h = rotateRight(h); } if (isRed(h.left) && isRed(h.right)) { flipColors(h); } h.N = size(h.left) + size(h.right) + 1; return h; }
除了递归调用后的三条if语句,红黑树中的put()的递归实现和二叉查找树中put()的实现完全相同。它们在查找路径上保证了红黑树和2-3树的一一对应关系,使得树的平衡性接近完美。第一条if语句会将任意含有红色右链接的3-结点(或临时的4-结点)向左旋转;第二条if语句会将临时的4-结点中两条连续红链接中的上层链接向右旋转;第三条if语句会进行颜色转换并将红链接在树中向上传递。