CF860E Arkady and a Nobody-men

CF860E Arkady and a Nobody-men 

类比LNOI2014 LCA那个题，其实树剖可以过。。。。（用树状数组区间加区间求和更快！）

巧妙的nlogn做法是：

blog~

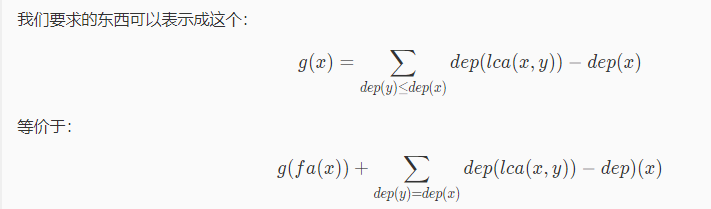（其实第二个式子有锅，应当再加上dep[fa[x]]）

对于同一层的考虑处理lca问题

一定要排个序处理

dfs是处理树上顺序的有力武器！

按dfs从小到大，一个x的前面的所有点的lca深度单调不降

可以用一个单调栈维护，只用维护：最后的位置（宽度），深度（键值），代表的点

如果和栈顶的代表点的lca深度比栈顶的键值小，那么pop栈顶，等价于把些点合并！

详见代码：

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('
');}
namespace Modulo{
const int mod=998244353;
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;}
}
//using namespace Modulo;
namespace Miracle{
const int N=5e5+5;
int n;
int fa[N][20];
ll g[N];
struct node{
    int nxt,to;
}e[N];
int hd[N],cnt;
void add(int x,int y){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
}
int dfn[N],df;
int dep[N];
vector<int>mem[N];
int mx;
void dfs(int x,int d){
    dep[x]=d;
    mx=max(mx,d);
    mem[d].pb(x);
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        dfs(y,d+1);
    }
}
struct po{
    int id,pos,d;
    po(){}
    po(int ii,int dd,int pp){
        id=ii;pos=pp;d=dd;
    }
}sta[N];
int top;
ll calc(){
    if(!top) return 0;
    return (ll)(sta[top].pos-sta[top-1].pos)*sta[top].d;
}
int lca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(reg j=19;j>=0;--j){
        if(dep[fa[x][j]]>=dep[y]) x=fa[x][j];
    }
    if(x==y) return x;
    for(reg j=19;j>=0;--j){
        if(fa[x][j]!=fa[y][j]) x=fa[x][j],y=fa[y][j];
    }
    return fa[x][0];
}
void sol(vector<int>&v){
    int o=0;
    top=0;
    ll val=0;
    for(solid x:v){
        if(!o){
            ++top;sta[top]=po(x,0,0);
        }
        else{
            while(1){
                int y=lca(sta[top].id,x);
                if(dep[y]>=sta[top].d){
                    ++top;sta[top]=po(x,dep[y],o);break;
                }
                val-=calc();
                --top;
            }
            val+=calc();
            g[x]+=val;
        }
        ++o;
    }
}
int main(){
    rd(n);
    int rt=0;
    for(reg i=1;i<=n;++i){
        rd(fa[i][0]);if(fa[i][0]==0) rt=i;
        else add(fa[i][0],i);
    }
    dfs(rt,1);
    for(reg j=1;j<=19;++j){
        for(reg i=1;i<=n;++i){
            fa[i][j]=fa[fa[i][j-1]][j-1];
        }
    }
    for(reg i=1;i<=mx;++i){
        for(solid x:mem[i]) g[x]=g[fa[x][0]]+i-1;
        sol(mem[i]);
        reverse(mem[i].begin(),mem[i].end());
        sol(mem[i]);
    }
    prt(g,1,n);
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
*/

LCA和dfs本身着关系，

这里利用的本质上是，两个点的lca就是dfs栈不断回溯后，第一次前进下来的点就是lca（分叉地方）

O(1)LCA也是利用这个性质