luoguP4707 重返现世

收集邮票加强版，每个邮票不是等概率获得的了。

而且是获得K个，如果把一个全集S集合找出其获得时间集合（显然获得时间两两不同）的话，那么就是第n-k+1大的期望！

%%%Sooke

min-max容斥扩展：

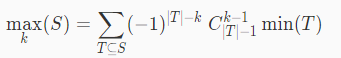
推广到期望：

只要求后面的东西

对于集合T，设∑t∈T=SUM，那么，E(min(T))=m/SUM

所以，只要知道SUM，就可以计算贡献

所以，不妨把SUM放进状态里，记录贡献次数（就是-1和组合数那坨）

k=n-k+1之后也很小

f[p][i][j]，当k=p时候，前i个，SUM=j的所有集合的贡献

i不加入：<-f[p][i-1][j]

i加入，[i-1][j]转移。p？之前的所有的这样的集合大小都+1了

就是考虑用组合数来巧妙推出|T|->|T|+1

然后就可以递推了！

初值：f[0][0][0]=0,f[k][0][0]=-1，或者手动把i=1的情况做出来也可以

滚动数组

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('
');}

namespace Miracle{
const int N=1005;
const int M=10000+5;
const int K=14;
const int mod=998244353;
int n,k,m;
int p[N];
int f[2][K][M];
int inv[M];
int ad(int x,int y){
    return x+y>=mod?x+y-mod:x+y;
}
int main(){
    rd(n);rd(k);rd(m);
    for(reg i=1;i<=n;++i) rd(p[i]);
    k=n-k+1;
    inv[1]=1;
    for(reg i=2;i<=m;++i) {
        inv[i]=(ll)(mod-mod/i)*inv[mod%i]%mod;
    }
    int tmp=0;
    for(reg t=1;t<=k;++t) f[tmp][t][0]=-1;
    for(reg i=1;i<=n;++i){
        tmp^=1;
        memset(f[tmp],0,sizeof f[tmp]);
        for(reg t=1;t<=k;++t){
            for(reg j=0;j<=m;++j){
                f[tmp][t][j]=f[tmp^1][t][j];
                if(j>=p[i]){
                    f[tmp][t][j]=ad(f[tmp][t][j],ad(f[tmp^1][t-1][j-p[i]],mod-f[tmp^1][t][j-p[i]]));
                }
            }
        }
    }
    ll ans=0;
    for(reg j=1;j<=m;++j){
        ans=ad(ans,(ll)f[tmp][k][j]*m%mod*inv[j]%mod);
    }
    cout<<ans;
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
*/