[学习笔记]长链剖分

处理和深度有关的一些事情

长链剖分的代码和重链剖分一样。只是重儿子条件不同罢了。

%%zzq

---

upda：2019.3.17

之前和没学一样。。。

 补充：

本质是优化DP，DP一维和深度有关

实现有一些类似dsu on tree

都是利用长链/重链保留下来的信息，减少时间/空间复杂度

长链剖分还有一个操作精髓是继承长儿子的信息

通常用指针分配内存，使得长儿子信息更新位置恰好是x的位置偏移一位

共用部分数组，相对独立又相互依存，这点和dsu on tree有不同

例题

用到的长链剖分性质：最长

使得：

1.利于分配内存

2.当前x的最大深度从长儿子继承过来，所以数组一定是最深的。减少讨论

3.k级祖先所在链长大于等于k

k级祖先

利用k级祖先的链一定长度大于等于k的条件。配合预处理倍增数组、链顶记录信息、二进制拆分出最高位。实现O(1)查询

因为长链之和是n,所以对每个长链处理的复杂度都是正确的。

CF1009F Dominant Indices 

模板题。最大值位置在更新时候进行偏移即可。

代码：

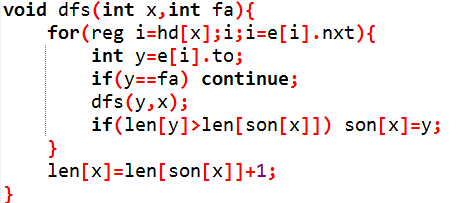
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('
');}

namespace Miracle{
const int N=1e6+6;
int son[N],len[N];
int n;
struct node{
    int nxt,to;
}e[2*N];
int hd[N],cnt;
int *f[N],memchi[N],ans[N],*cur=memchi;
void add(int x,int y){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
}
void dfs(int x,int fa){
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dfs(y,x);
        if(len[y]>len[son[x]]) son[x]=y;
    }
    len[x]=len[son[x]]+1;
}
void dp(int x,int fa){
    f[x][0]=1;
    if(son[x]) f[son[x]]=f[x]+1,dp(son[x],x),ans[x]=ans[son[x]]+1;
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa||y==son[x]) continue;
        f[y]=cur;cur+=len[y];
        dp(y,x);
        for(reg j=1;j<=len[y];++j){
            f[x][j]+=f[y][j-1];
            if((j<ans[x]&&f[x][j]>=f[x][ans[x]])||(j>ans[x]&&f[x][j]>f[x][ans[x]])) ans[x]=j;
        }
    }
    if(f[x][0]==f[x][ans[x]]) ans[x]=0;
}
int main(){
    rd(n);
    int x,y;
    for(reg i=1;i<n;++i){
        rd(x);rd(y);add(y,x);add(x,y);
    }
    dfs(1,0);
    f[1]=cur;cur+=len[1];
    dp(1,0);
    for(reg i=1;i<=n;++i){
        printf("%d
",ans[i]);
    }
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2019/3/17 15:44:31
*/

cogs 秘术

0/1分数规划，二分答案，记录深度为j的点权和最小值，m是固定的，直接更新答案

平移数组，整体加上ci，用tag[x]维护整体加

bzoj4543 Hotel 加强版

主要还是DP式子吧，，，

bzoj3522: [Poi2014]Hotel

某fzyzoj题

n<=1e6个点，边权为1，求树上不超过L的链的条数

f[x][j]，长度小于等于j的点的个数

可以利于我们枚举y的一边，直接贡献答案。

合并有点苟，因为是一个前缀和，所以不断更新tag[x]，len[x]>len[y]的超过的部分，都加上f[y][len[y]-1]。

代码：

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('
');}

namespace Miracle{
const int N=1000000+5;
int n,L;
struct node{
    int nxt,to;
}e[2*N];
int hd[N],cnt;
void add(int x,int y){
    e[++cnt].nxt=hd[x];
    e[cnt].to=y;
    hd[x]=cnt;
}
int *f[N],memchi[N],*cur=memchi;
int len[N],son[N];
int tag[N];
void dfs(int x,int fa){
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa) continue;
        dfs(y,x);
        if(len[y]>len[son[x]]) son[x]=y;
    }
    len[x]=len[son[x]]+1;
}
ll ans;
void dp(int x,int fa){
    if(son[x]) f[son[x]]=f[x]+1,dp(son[x],x),f[x][0]=-tag[son[x]],ans+=f[son[x]][min(L-1,len[son[x]]-1)]+tag[son[x]];
    tag[x]=tag[son[x]]+1;
    for(reg i=hd[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(y==fa||y==son[x]) continue;
        f[y]=cur;cur+=len[y];
        dp(y,x);
        for(reg j=0;L-j-1>=0&&j<len[y];++j){
            if(j) ans+=((ll)f[y][j]-f[y][j-1])*((ll)f[x][min(len[x]-1,L-j-1)]+tag[x]);
            else ans+=((ll)f[y][j]+tag[y])*((ll)f[x][min(len[x]-1,L-j-1)]+tag[x]);
        }
        ll tmp=f[y][len[y]-1]+tag[y];
        for(reg j=1;j<=len[y];++j){
            f[x][j]+=f[y][j-1]+tag[y]-tmp;
        }
        f[x][0]-=tmp;
        tag[x]+=tmp;
    }
//    cout<<" infor "<<x<<endl;
//    for(reg i=0;i<len[x];++i){
//        cout<<f[x][i]<<" ";
//    }cout<<endl;
//    cout<<" tag "<<tag[x]<<endl;
}
int main(){
    rd(n);rd(L);
    int x,y;
    for(reg i=1;i<n;++i){
        rd(x);rd(y);add(x,y);add(y,x);
    }
    dfs(1,0);
//    prt(len,1,n);
//    prt(son,1,n);
    f[1]=cur;cur+=len[1];
    dp(1,0);
    printf("%lld",ans);
    return 0;
}

}
signed main(){
//    freopen("data.in","r",stdin);
//    freopen("my.out","w",stdout);
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
   Date: 2019/3/17 18:10:50
*/

长链剖分思想是基于和深度有关的DP

dsu on tree思想是莫队，全局数据结构维护，暴力添加子树删除子树

dsu on tree由于可以全局维护并且子树暴力查询，可以做的事情是长链剖分的超集

但是长链剖分在特殊情况下的O(n)是无法超越的