拉格朗日插值法(图文详解)
自我感觉挺实用的一个算法。
也为一些题目提供了解决的思路。
插值:给一些散点,求满足这些个散点的函数(多项式),即求出这些系数
一般求一个点值,都要先得到系数,再O(n)算。求系数,高斯消元,是O(n^3)的。
但是,如果只要一个点值,这样岂不是血亏。
拉格朗日这个人比较厉害,他发明的算法,可以在不用求出具体系数的情况下,O(n^2)的计算一个位置的点值。
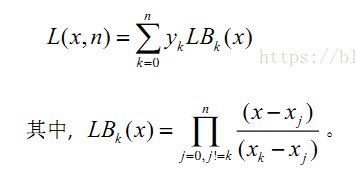
思想类似于互质的CRT,
对于给定n+1个点值,这个多项式最多n次的。而且,把每个横坐标带进去,xi自己的一项得到yi,别的由于分子有xi-xi,都是0
所以,这个多项式一定和实际上的多项式是一个多项式。
然后我们把要求的x带进去,就得到了函数值。
有什么用?
如果证明一个式子的函数是n次多项式的话,那么可以尝试得到n+1个点值,然后弄出这个公式,就可以计算比较大的答案。
https://blog.csdn.net/xyz32768/article/details/81233900
这个题,很大数据范围的k次方和,第一没有办法反演。第二没有规律可以找。
猜这个求和函数是一个k+1次多项式。然后带点求值,然后对目标答案的计算进行化简。
从O(n)到O(k^2)到O(klogk)(然鹅这个logk是因为点值的快速幂,后面的计算不是瓶颈23333)
突破口
1.想到是一个多项式
2.点值的取值是有讲究的,1~k+2这样连续的整点有助于预处理减少复杂度(跟自己干嘛要过不去23333)
所以,拉格朗日插值这个公式其实很整齐,
如果点值横坐标给的很好的话(支持递推),那么可以在O(n)时间求出一个值。已经非常不错了。
CF622F The Sum of the k-th Powers
代码:

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=1e6+5; const int mod=1e9+7; int n,k; int qm(int x,int y){ int ret=1; while(y){ if(y&1) ret=(ll)ret*x%mod; x=(ll)x*x%mod; y>>=1; } return ret; } ll pre[N],bac[N]; ll fu[N]; ll y[N]; ll sol(){ ll ret=0; for(reg i=1;i<=k+2;++i){ //cout<<" i "<<i<<" : "<<y[i]<<" "<<pre[i-1]<<" "<<pre[k+2-i]<<" "<<bac[k+2]<<" "<<n-i<<endl; if(n>k+2) ret=(ret+y[i]*qm(pre[i-1]*(fu[k+2-i])%mod,mod-2)%mod*(bac[k+2]*qm((n-i),mod-2)%mod)%mod)%mod; else { if(n!=i) ret=(ret+y[i]*qm(pre[i-1]*(fu[k+2-i])%mod,mod-2)%mod*(bac[k+2]*qm(((n-i)+mod)%mod,mod-2)%mod)%mod)%mod; else ret=(ret+y[i])%mod; } // cout<<" ret "<<ret<<endl; } return ret; } int main(){ rd(n);rd(k); pre[0]=1; bac[0]=1; fu[0]=1; y[0]=0; for(reg i=1;i<=k+2;++i){ pre[i]=pre[i-1]*i%mod; fu[i]=fu[i-1]*(mod-i)%mod; bac[i]=(bac[i-1]*(n-i)%mod+mod)%mod; y[i]=(y[i-1]+qm(i,k))%mod; } printf("%lld",sol()); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2019/1/16 15:31:40 */
upda:2019.2.18
如果要找到真正的系数:
可以快速插值O(nlogn),非常难写
一个比较实用的是O(N^2)的背包:
考虑拉格朗日插值的公式的每一个f(i)项对每个系数的贡献
$f(i) frac{Pi_{j!=i}(x-x_j)}{Pi_{j!=i}(x_i-x_j)}$
分母是定值,$f(i)$是定值
分子不同之间差不多,
计算:$Pi(x-x_j)$再每次O(N)除以$(x-x_i)$
计算方法:
对每一项的贡献就是选择k个x,剩下n-k个选择$-x_j$这样
所以背包:$f[i][j]$表示前i个“括号”,x次幂是j的权值之和
$f[i][j]=f[i-1][j]*(-x_i)+f[i-1][j-1]$
O(N^2)
还有一种更容易实现的方法:
$f*(x-x_i)=f*x-f*x_i$也就是f平移一位,然后减掉自己原来的xi倍
递推即可实现。
还原时候除法,就是倒着回退一次即可。
