题意:一共有n名员工, n-1条关系, 每次给一个人分配任务的时候,(如果他有)给他的所有下属也分配这个任务, 下属的下属也算自己的下属, 每次查询的时候都输出这个人最新的任务(如果他有), 没有就输出-1。
题解:需要用DFS建树来确立关系, 然后用线段树进行区间覆盖。
DFS建树: 从Boss 开始dfs,通过dfs递归时编号出现的先后顺序来确定某个员工对应的起点与终点。
样例的关系图是这样的

当dfs建树跑完了之后各个节点对应的位置是这样的
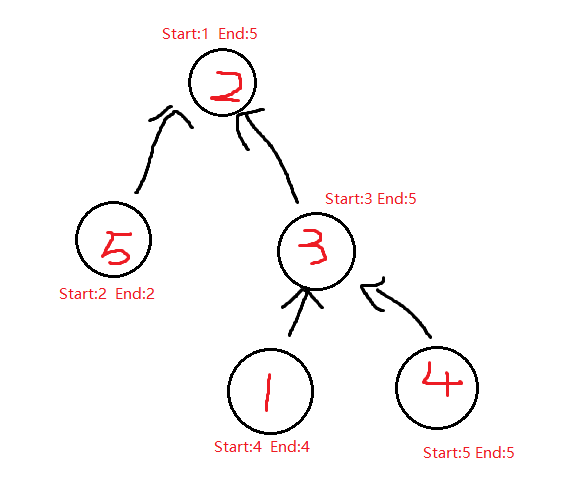
其中Start表示这个节点本身的新编号和这个节点管辖区间内的左端点 End表示这个点管辖区间内的右端点
从右边的图中可以看见其中的最上级2号员工(Boss), 他的管辖区间是[1,5],能覆盖所有人的结点, 5号员工他没有下属所以他的End值就等于Start值。
(发布于第二天的修改, 竟然被吐槽写的不好理解, 非要我再加上下面这幅图)
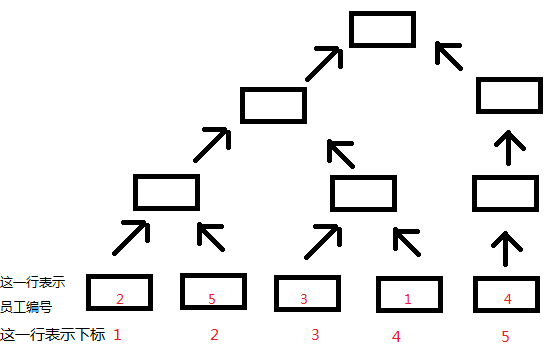
上面这幅图呢就是线段树下的员工状态图了, 假设我们现在对2号员工分配任务y1
那我们就需要对2号员工的管辖区域[1,5]区间的值都修改成y1。
再注意一下 管辖区域的左端点 还代表的这名员工在线段树下的区间下标是多少。
2号员工的管辖区域是[1,5] 所以他就在位置1。
管辖区域的右端点就是自己最多能管到员工的编号。
所以每次对自己的管辖区域进行线段树区域更新操作就可以将每个人的任务分配下去了。
这样每次查询某个员工的任务的时候只需要将lazy标记推到底,就能找到最后收到的任务了。
用DFS去访问每个节点,并将访问的顺序编号,当DFS遍历了整个关系图之后,每个人的管辖区间就确定下来了,然后就可以通过管辖区间来进行线段树区域覆盖和单点查询操作。
1 int cnt = 0; 2 void dfs(int n) 3 { 4 Start[n] = ++cnt; 5 int m = son[n].size(); 6 for(int i = 0; i < m; i++) 7 dfs(son[n][i]);//已经用vector son[n] 来存好了每个人的下属 8 End[n] = cnt; 9 }
1 #include<iostream> 2 #include<algorithm> 3 #include<vector> 4 #include<string> 5 #include<cstring> 6 #define lson l,m,rt<<1 7 #define rson m+1,r,rt<<1|1 8 using namespace std; 9 const int N = 50000+5; 10 vector<int> son[N]; 11 int Start[N], End[N]; 12 int tree[N<<2], lazy[N<<2]; 13 bool vis[N]; 14 int cnt = 0; 15 void dfs(int n) 16 { 17 Start[n] = ++cnt; 18 int m = son[n].size(); 19 for(int i = 0; i < m; i++) 20 dfs(son[n][i]); 21 End[n] = cnt; 22 } 23 void PushDown(int rt) 24 { 25 if(lazy[rt] != -1) 26 { 27 tree[rt<<1] = tree[rt<<1|1] = lazy[rt<<1|1] = lazy[rt<<1] = lazy[rt]; 28 lazy[rt] = -1; 29 } 30 } 31 void Revise(int L, int R, int C, int l, int r, int rt) 32 { 33 if(L <= l && r <= R) 34 { 35 lazy[rt] = tree[rt] = C; 36 return ; 37 } 38 PushDown(rt); 39 int m =l+r >> 1; 40 if(L <= m) Revise(L,R,C,lson); 41 if(m < R) Revise(L,R,C,rson); 42 } 43 int Query(int L, int l, int r, int rt) 44 { 45 if(l == r) 46 { 47 return tree[rt]; 48 } 49 int m = l+r >> 1; 50 PushDown(rt); 51 if(L <= m) return Query(L,lson); 52 else return Query(L,rson); 53 } 54 int main() 55 { 56 ios::sync_with_stdio(false); 57 cin.tie(0); 58 cout.tie(0); 59 int T; 60 cin >> T; 61 for(int i = 1; i <= T; i++) 62 { 63 cout << "Case #" << i << ": "; 64 int n, u, v; 65 cnt = 0; 66 cin >> n; 67 for(int i = 1; i <= n; i++) 68 son[i].clear(), vis[i] = 1; 69 for(int i = 1; i < n; i++) 70 { 71 cin >> u >> v; 72 son[v].push_back(u);//用vector去对应的关系 73 vis[u] = 0;//如果某个点成为过下属就标记一下 没有标记过的那个人就是Boss(最上级) 74 } 75 int pos = -1; 76 for(int i = 1; i <= n; i++) 77 if(vis[i]) 78 { 79 pos = i; 80 break; 81 } 82 dfs(pos);//从最上级的人开始递归, 找到每个人对应的区间 83 memset(tree, -1, sizeof(tree));//因为没有接到任务过的人查询的时候输出-1 84 memset(lazy, -1, sizeof(lazy));//所以直接memset为-1就好了,不需要再进行特判 85 int t; 86 cin >> t; 87 string str; 88 int x, y; 89 while(t--) 90 { 91 cin >> str; 92 if(str[0] == 'C') 93 { 94 cin >> x; 95 cout << Query(Start[x],1,cnt,1) << endl; 96 } 97 else 98 { 99 cin >> x >> y; 100 Revise(Start[x],End[x],y,1,cnt,1); 101 } 102 } 103 } 104 return 0; 105 }