题解:
树DP, 枚举每2个点作为国家。 然后计算出最小的答案。
首先我们枚举根, 枚举根了之后, 我们算出每个点的子树内部和谐之后的值是多少。
这样val[root]就是这个root为根的花费。
然后我们再fdfs一遍这棵树。
假如我们枚举u这个点是另一个国家,
则花费就是
1. root --- u 的路径上 保证路径上的点可以从 u 走到 或者就是 root 出发走到。
这个东西可以通过O1求得。
我们假设一个数组 记录下 root ---- u 之间的边。
1 表示为是正向边, -1表示为 反向边。
则我们需要这个数列修改完边的结果为 +++++ ------ 不能出现+-+ 或者 -+-。
现在假设这个数列的长度为len。
我们需要找到一个i 使得 1 <= i 的数都是 1, >i && <= n的数都是 -1。
那对于这个i的花费就是 (i-sum[i])/2 + ( (len-i)-(sum[len] - sum[i])) => (len + sum[len])/2 - sum[i]。 sum为这个数列的前缀和。
可以发现枚举完某个点之后, len + sum[len]都是定值, 需要找到最大的sum[i]就好了, 并且这个sum[i]前面不会改变, 所以我们这个sum[i]也可以做个前缀和, 找到最大的那个值。
2. val[u]
也就是使得u子树和谐的花费。
3. tmp_val
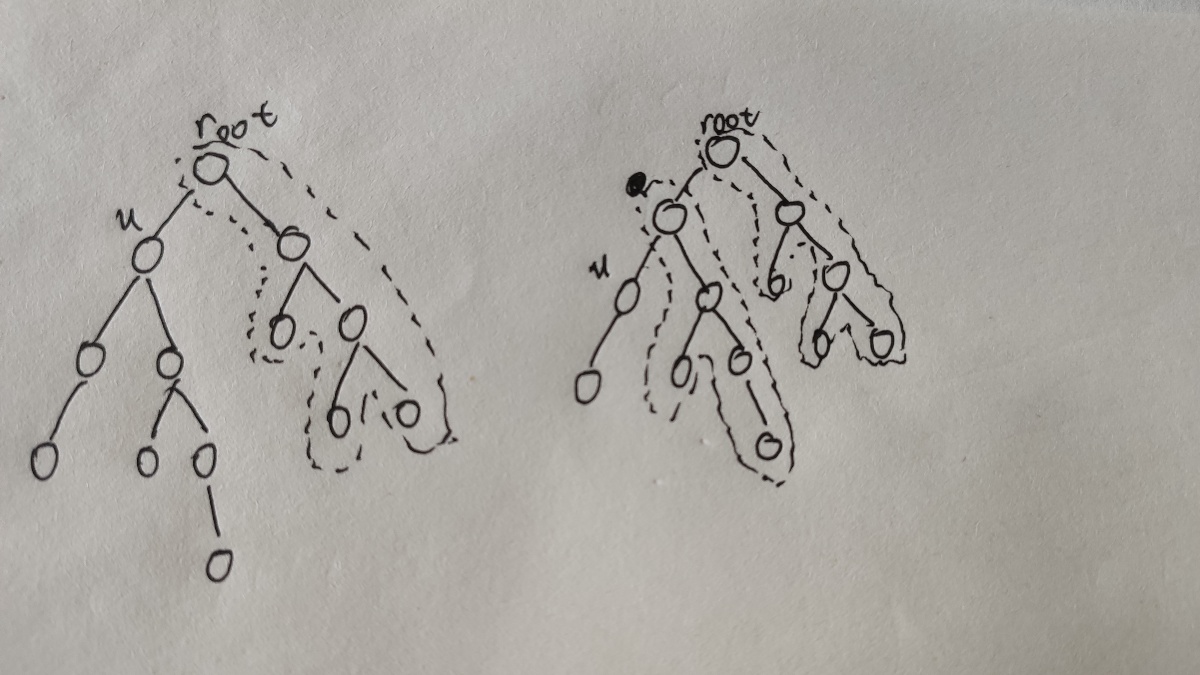
使得除了 root --- u路径上的点都和谐的花费。
也就是上图中的 虚线框起来的边的花费。
这3块总和就是答案了。
然后在所有枚举的过程中找最小值。
代码:

#include<bits/stdc++.h> using namespace std; #define Fopen freopen("_in.txt","r",stdin); freopen("_out.txt","w",stdout); #define LL long long #define ULL unsigned LL #define fi first #define se second #define pb push_back #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define lch(x) tr[x].son[0] #define rch(x) tr[x].son[1] #define max3(a,b,c) max(a,max(b,c)) #define min3(a,b,c) min(a,min(b,c)) typedef pair<int,int> pll; const int inf = 0x3f3f3f3f; const int _inf = 0xc0c0c0c0; const LL INF = 0x3f3f3f3f3f3f3f3f; const LL _INF = 0xc0c0c0c0c0c0c0c0; const LL mod = (int)1e9+7; const int N = 4e3; vector<pll> vc[N]; int val[N]; int ans = inf; int tmp_val = 0; void dfs(int o, int u){ val[u] = 0; for(pll t : vc[u]){ int v = t.fi; if(v == o) continue; dfs(u, v); val[u] += val[v] + (t.se == -1); } } void fdfs(int deep, int sum, int Max, int o, int u){ if(o){ ans = min(ans, (deep+sum)/2 - Max+tmp_val+val[u]); } for(pll t : vc[u]){ int v = t.fi; if(v == o) continue; tmp_val += val[u] - (val[v] + (t.se == -1)); fdfs(deep+1, sum+t.se, max(Max, sum+t.se),u, v); tmp_val -= val[u] - (val[v] + (t.se == -1)); } } int main(){ int n; scanf("%d", &n); for(int i = 1, u, v; i < n; ++i){ scanf("%d%d", &u, &v); vc[u].pb(make_pair(v, 1)); vc[v].pb(make_pair(u,-1)); } for(int i = 1; i <= n; ++i){ dfs(0, i); ans = min(ans, val[i]); tmp_val = 0; fdfs(0, 0, 0,0, i); } cout << ans << endl; return 0; }
