堆
优先级队列是一种抽象数据结构(ADT)。
优先级队列可以用数组实现,删除最大或最小值的效率是O(1),但插入数据的效率是O(N)。
堆是优先级队列的另一种实现
椎的效率
堆是一种树,插入删除都是O(logN),不支持查询
堆的特点
1、完全二叉树,即每一层从左到右都是满的。
2、常用数组实现。使用数组而不是使用引用连接各个节点。
3、每个节点的关键字都大于或等于它子节点的关键字。
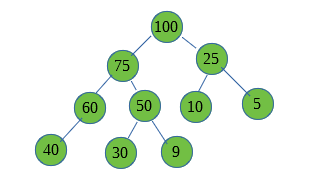
这不是一颗完全二叉树,仅仅因为60没有右子节点。
分析堆的特点
完全二叉树,表示堆的数组没有洞。
从根节点到任何叶子节点都是降序。
弱序:
1、不支持顺序遍历
2、不能在堆上便利地查找指定的关键字,因为没有足够的信息来决定走两个子节点的哪个路径
3、不支持删除指定关键字的节点,因为查不到
接近无序,不过,可以快速删除最大或最小节点,快速插入。
堆的实现
数组实现,若数组中某节点的下标是x,其父节点的下标为 (x-1)/2;左子节点下标为 (2*x)+1;右子节点下标为 (2*x)+2。
二叉树实现,找到最后插入的元素:事实证明,树中节点数目的二进制表示,与最后插入元素相关。假设树有29个节点,29=11101,移除开头的1,剩下1101,0向左,1向右,从根节点向右、向右、向左、向右。
删除最大最小节点
1、删除根节点,树不是完全树了,或者数组里有了一个洞。
2、可以把数组里所有的数据项都向前移动一位;但还有更快的方法。
a、把最后插入的元素移动到根
b、比较根元素的两个子节点,再比较较大的子节点和根节点。
c、如果根节点小,两个元素换位置;持续...
最后一个插入的元素并不总是最终被移动到最底层,有时它会停留在中间某层
插入新元素
1、把新元素添加到最后一个位置
2、把新元素和父节点比较,新节点大,交换位置;新节点小,结束。
插入的比较且交换位置的算法比删除的简单,因为只需新节点和父节点相比较就可以;在删除时,还需要比较两个子节点的大小。
交换位置

第一个图,交换a、b位置,要复制三次;交换a、c的位置,再复制三次,a、d又三次;共九次复制。
第二个图,把a复制到空节点缓存,复制b到a,复制c到b,复制d到c,复制a到d;共五次复制。