树、多路树、二叉树

树

结合了有序数组和链表的优点。在树中查询和在有序数组中一样快；插入和删除和链表一样快。

遍历相对比较慢一点。

从根到其它任何一个节点有且只有一条路径，比如下面的图示不是树：

多路树

每个节点的子节点可以多于两个

二叉树

每个节点的子节点最多有两个

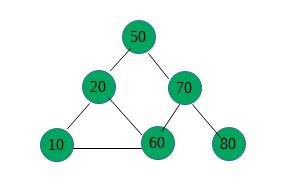
二叉搜索树

一个节点的左子节点的数小于该节点，右子节点的数大于或等于该父节点

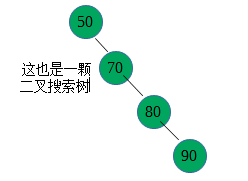
其它二叉树

二叉树并不全是搜索树。二叉树可以用于表示代数表达式，还可以用于哈夫曼编码以令人惊讶的方式压缩数据。

二叉搜索树的代码

class Node {
    public int iData;
    public double dData;
    public Node leftChild;
    public Node rightChild;

    public void displayNode() {
        System.out.print('{');
        System.out.print(iData);
        System.out.print(", ");
        System.out.print(dData);
        System.out.print("} ");
    }
}

class Tree {
    private Node root;
    public Tree() {
        root = null;
    }
    /* 前序遍历
     * 二叉树(不是二叉搜索树)可以表示包括二元操作符的算术表达式。
     *             *
     *          a     +
     *              b   c 
     * 中序遍历会得到中序表达式，不过要自己加括号
     * 前序遍历会得到前序表达式
     * 后序遍历会得到后序表达式
     */
    private void preOrder(Node localRoot) {
        if (localRoot != null) {
            System.out.print(localRoot.iData + " ");
            preOrder(localRoot.leftChild);
            preOrder(localRoot.rightChild);
        }
    }
    // 中序遍历，最常用，如果是二叉搜索树结果升序。
    private void inOrder(Node localRoot) {
        if (localRoot != null) {
            inOrder(localRoot.leftChild);
            System.out.print(localRoot.iData + " ");
            inOrder(localRoot.rightChild);
        }
    }
    // 后序遍历
    private void postOrder(Node localRoot) {
        if (localRoot != null) {
            postOrder(localRoot.leftChild);
            postOrder(localRoot.rightChild);
            System.out.print(localRoot.iData + " ");
        }
    }
    // 插入
    public void insert(int id, double dd) {
        Node newNode = new Node();
        newNode.iData = id;
        newNode.dData = dd;
        if (root == null)
            root = newNode;
        else {
            Node current = root;
            Node parent;
            while (true) {
                parent = current;
                if (id < current.iData) {
                    current = current.leftChild;
                    if (current == null) {
                        parent.leftChild = newNode;
                        return;
                    }
                }  
                else {
                    current = current.rightChild;
                    if (current == null) {
                        parent.rightChild = newNode;
                        return;
                    }
                }  
            }
        }
    }
    // 查找
    public Node find(int key) {
        Node current = root;
        while (current.iData != key) {
            if (key < current.iData)
                current = current.leftChild;
            else
                current = current.rightChild;
            if (current == null)
                return null;
        }
        return current;
    }
    // 删除
    public boolean delete(int key) {
        Node current = root;
        Node parent = root;
        boolean isLeftChild = true;

        while (current.iData != key) {
            parent = current;
            if (key < current.iData) {
                isLeftChild = true;
                current = current.leftChild;
            } else {
                isLeftChild = false;
                current = current.rightChild;
            }
            if (current == null)
                return false;
        }
        if (current.leftChild == null &&
                current.rightChild == null) {
            if (current == root)
                root = null;
            else if (isLeftChild)
                parent.leftChild = null;
            else
                parent.rightChild = null;
        } else if (current.rightChild == null)
            if (current == root)
                root = current.leftChild;
            else if (isLeftChild)
                parent.leftChild = current.leftChild;
            else
                parent.rightChild = current.leftChild;


        else if (current.leftChild == null)
            if (current == root)
                root = current.rightChild;
            else if (isLeftChild)
                parent.leftChild = current.rightChild;
            else
                parent.rightChild = current.rightChild;

        else {
            Node successor = getSuccessor(current);
            if (current == root)
                root = successor;
            else if (isLeftChild)
                parent.leftChild = successor;
            else
                parent.rightChild = successor;
            successor.leftChild = current.leftChild;
        }
        return true;
    }
    private Node getSuccessor(Node delNode) {
        Node successorParent = delNode;
        Node successor = delNode;
        Node current = delNode.rightChild;
        while (current != null) {
            successorParent = successor;
            successor = current;
            current = current.leftChild;
        }

        if (successor != delNode.rightChild) {
            successorParent.leftChild = successor.rightChild;
            successor.rightChild = delNode.rightChild;
        }
        return successor;
    }
    public void traverse(int traverseType) {
        switch (traverseType) {
            case 1:
                System.out.print("
Preorder traversal: ");
                preOrder(root);
                break;
            case 2:
                System.out.print("
Inorder traversal:  ");
                inOrder(root);
                break;
            case 3:
                System.out.print("
Postorder traversal: ");
                postOrder(root);
                break;
        }
        System.out.println();
    }
    public void displayTree() {
        Stack globalStack = new Stack();
        globalStack.push(root);
        int nBlanks = 32;
        boolean isRowEmpty = false;
        System.out.println(
                "......................................................");
        while (isRowEmpty == false) {
            Stack localStack = new Stack();
            isRowEmpty = true;

            for (int j = 0; j < nBlanks; j++)
                System.out.print(' ');

            while (globalStack.isEmpty() == false) {
                Node temp = (Node) globalStack.pop();
                if (temp != null) {
                    System.out.print(temp.iData);
                    localStack.push(temp.leftChild);
                    localStack.push(temp.rightChild);

                    if (temp.leftChild != null ||
                            temp.rightChild != null)
                        isRowEmpty = false;
                } else {
                    System.out.print("--");
                    localStack.push(null);
                    localStack.push(null);
                }
                for (int j = 0; j < nBlanks * 2 - 2; j++)
                    System.out.print(' ');
            }  // end while globalStack not empty
            System.out.println();
            nBlanks /= 2;
            while (localStack.isEmpty() == false)
                globalStack.push(localStack.pop());
        }  // end while isRowEmpty is false
        System.out.println(
                "......................................................");
    }
}

树的效率

节点数	层数
1	1
3	2
7	3
15	4
31	5
...	...
1023	10
...	...
32767	15
...	...
1048575	20
...	...
33554432	25
...	...
1073741824	30

  

如果一颗树是绝对平衡的满树，该树有L层，那么最差的查询效率是L次。
设表中节点数是N，层数是L，则N = 2^L - 1；L = log₂(N+1)，大致为L=Log₂N 。因此，常见的树的操作时间复杂度大致是O(LogN)。
如果树不满，分析起来比较困难。不过，在这种情况下，在较低层查找的次数要少。