朋友圈
题目背景
小奇采的矿实在太多了,它准备在喵星系建个矿石仓库。令它无语的是,喵星系的货运飞船引擎还停留在上元时代!
题目内容
喵星系有(n)个星球,星球以及星球间的航线形成一棵树。
从星球(a)到星球(b)要花费([ ext{dis}(a,b) ext{xor} M])秒。(( ext{dis}(a,b))表示ab间的航线长度,( ext{xor})为位运算中的异或)
为了给仓库选址,小奇想知道,星球(i(1leq ileq n))到其它所有星球花费的时间之和。
数据范围
(6leq nleq 100000,0leq Mleq 15)
思路
出题人:
算法1:
不会写函数的小伙伴们,我们只需要写个floyd,就有10分啦!
算法2:
在算法1的基础上,我们对每条边处理一下xor,就有20分啦!
算法3:
简单的树形DP,或者你会nlogn的dij,处理完每个点到其它点的最短路后再加上xor,那么这样就有30分啦!
算法4:
第4、5个点无需xor,那么我们树形DP扫一个节点与其它所有节点的路径长度之和,可以合并信息,最终均摊O(1),50分到手。
算法5:
第6个点xor 1,那么我们树形DP到一个点时记录有多少个0,多少个1,然后每当一条路径到2,那部分就再记录一个值,60分到手。
算法6:
如果你第6个点都过了,却没有满分,笨死啦!
一样的嘛,就是原来的“0”、“1”、大于等于2变成了0~16么~~
满了。
我:?
考场上直接打的(O(n^2))枚举区间再加上求( ext{LCA})的复杂度的暴力,结果一时脑瘫建边的时候就异或了(M)结果惨挂(10pts),然后考后改成最后再异或就(30pts)了...(差点有比郭神高的机会呢qwq)
然后正解是换根(dp),又是假期埋下的一个坑吗
先考虑没有异或的情况。设已经搜到了边(<u,v,w>),且(u)是(v)的父亲,那么如何更新(ans[v])呢?
当然你会选择合并同类项,不过先不合并比较好理解,对于(u)以上的节点,其个数为(n-size[v]),对于原来的(ans[u])距离多了一个(w),所以加上((n-size[v]) imes w),对于(v)的子树节点,对(v)的距离就是其到(u)的距离减去(w),所以就能得到以上的柿子。
大概这个样子:
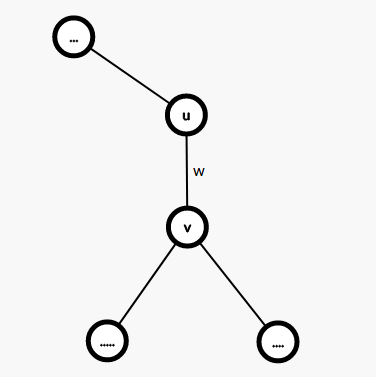
然而本题要求异或,由我惨挂10分的经历可以知道异或并不满足分配律,所以并不能边加边异或。然而可以看出(Mleq 15),转换为二进制为(1111),所以最后异或(M)的时候仅会对后四位有影响,所以只需要记录后四位的状态即可。
设(f[i][j])表示到了(i)点,当前后四位的状态为(j),能伸展出的路径条数。
对于初始:(f[u][0]=1),表示自己到自己为一条路径。为了方便,你可以先加上自己然后最后减去。
然后就是(f[u][(j+w) \% 16]+=f[v][j]),从子树转移过来。
然而除了子树以外还有别的点,如何转移呢?
很容易理解,对于(v)的父亲(u),先刨去子树(v)的贡献,然后剩下的就是其他点到(u)的贡献,你再通过(<u,v,w>)边转移到(v)上,再加上原来就有的(v)的子树的,就是整棵树到(v)的贡献。
最后你再异或个(M)即可。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,M;
long long f[maxn][20],ans[maxn],a[20];
struct Edge{
int from,to,w,nxt;
}e[maxn<<1];
inline int read(){
int x=0,fopt=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')fopt=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+ch-48;
ch=getchar();
}
return x*fopt;
}
int head[maxn],cnt;
inline void add(int u,int v,int w){
e[++cnt].from=u;
e[cnt].to=v;
e[cnt].w=w;
e[cnt].nxt=head[u];
head[u]=cnt;
}
void dfs1(int u,int fa){
f[u][0]=1;
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to;
if(v==fa)continue;
dfs1(v,u);
ans[u]+=ans[v];
for(int j=0;j<=15;j++){
int w=e[i].w;
f[u][(j+w)%16]+=f[v][j];
ans[u]+=f[v][j]*w;
}
}
}
void dfs2(int u,int fa){
for(int i=head[u];i;i=e[i].nxt){
int v=e[i].to,w=e[i].w;
if(v==fa)continue;
memset(a,0,sizeof(a));//临时先开个数组存一下,因为下面还要加siz,最好不要直接更新
int siz=0;
for(int j=0;j<=15;j++){
a[(j+w)%16]+=f[u][j]-f[v][((j-w)%16+16)%16];//防止下标变负
siz+=f[v][j];
}
ans[v]=ans[u]+(n-2*siz)*w;
for(int j=0;j<=15;j++)
f[v][j]+=a[j];
dfs2(v,u);
}
}
int main(){
freopen("B.in","r",stdin);
freopen("B.out","w",stdout);
n=read();M=read();
for(int i=1;i<n;i++){
int u=read(),v=read(),w=read();
add(u,v,w);
add(v,u,w);
}
dfs1(1,0);
dfs2(1,0);
for(int i=1;i<=n;i++){
f[i][0]--;//刨去到自己的路径
for(int j=0;j<=15;j++)
ans[i]+=((j^M)-j)*f[i][j];//加上异或后相差的值,另外还是老问题异或的优先级
printf("%lld
",ans[i]);
}
return 0;
}