20162309《程序设计与设计结构》第十周学习总结

学号 20162309 《程序设计与数据结构》第10周学习总结

教材学习内容总结

关于堆：
在计算机领域，堆栈是一个不容忽视的概念，堆栈是两种数据结构。堆栈都是一种数据项按序排列的数据结构，只能在一端(称为栈顶(top))对数据项进行插入和删除。在单片机应用中，堆栈是个特殊的存储区，主要功能是暂时存放数据和地址，通常用来保护断点和现场。要点：堆，队列优先,先进先出（FIFO—first in first out）[1]  。栈，先进后出(FILO—First-In/Last-Out)。
关于堆栈的问题：
堆栈空间分配
栈（操作系统）：由操作系统自动分配释放 ，存放函数的参数值，局部变量的值等。其操作方式类似于数据结构中的栈。
堆（操作系统）： 一般由程序员分配释放， 若程序员不释放，程序结束时可能由OS回收，分配方式倒是类似于链表。
堆栈数据结构区别
堆（数据结构）：堆可以被看成是一棵树，如：堆排序。
栈（数据结构）：一种先进后出的数据结构。
关于堆栈的区别介绍：

1. 栈(stack)与堆(heap)都是Java用来在Ram中存放数据的地方。与C++不同，Java自动管理栈和堆，程序员不能直接地设置栈或堆。
2. 栈的优势是，存取速度比堆要快，仅次于直接位于CPU中的寄存器。但缺点是，存在栈中的数据大小与生存期必须是确定的，缺乏灵活性。另外，栈数据在多个线程或者多个栈之间是不可以共享的，但是在栈内部多个值相等的变量是可以指向一个地址的，详见第3点。堆的优势是可以动态地分配内存大小，生存期也不必事先告诉编译器，Java的垃圾收集器会自动收走这些不再使用的数据。但缺点是，由于要在运行时动态分配内存，存取速度较慢。
   数据类型包装类的值不可修改。不仅仅是String类的值不可修改，所有的数据类型包装类都不能更改其内部的值。
   相关定义：
   堆通常是一个可以被看做一棵树的数组对象。
   堆（英语：heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：
   堆中某个节点的值总是不大于或不小于其父节点的值；
   堆总是一棵完全二叉树。
   将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
   堆的定义如下：n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时，称之为堆。
   (ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4...n/2)
   若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。由此，若序列{k1,k2,…,kn}是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。
   关于优先队列：
   普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征。
   定义：优先队列的类定义

优先队列是0个或多个元素的集合,每个元素都有一个优先权或值,对优先队列执行的操作有1) 查找;2) 插入一个新元素;3) 删除.在最小优先队列(min priority queue)中,查找操作用来搜索优先权最小的元素,删除操作用来删除该元素;对于最大优先队列(max priority queue),查找操作用来搜索优先权最大的元素,删除操作用来删除该元素.优先权队列中的元素可以有相同的优先权,查找与删除操作可根据任意优先权进行。
关于图 ：
无向图的实例

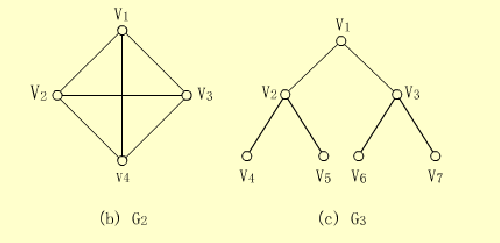
关于无向图的概念解释：
直观来说，若一个图中每条边都是无方向的，则称为无向图。
无向图中的边均是顶点的无序对，无序对通常用圆括号表示。

教材学习中的问题和解决过程

• 问题：十字链表的相关概念和使用
• 问题解决方案：
  关于十字链表：十字链表(Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。用十字链表来存储有向图，可以达到高效的存取效果。同时，代码的可读性也会得到提升。用链表模拟矩阵的行(或者列，这可以根据个人喜好来定)，然后，再构造代表列(或者是行)的链表，将每一行中的元素节点插入到对应的列中去。十字链表的逻辑结构就像是一个围棋盘(没见过，你就想一下苍蝇拍，这个总见过吧!)，而非零元就好像是在棋盘上放的棋子，总共占的空间就是，确定那些线的表头节点和那些棋子代表的非零元节点。最后，我们用一个指针指向这个棋盘，这个指针就代表了这个稀疏矩阵，此为十字链表的构成。

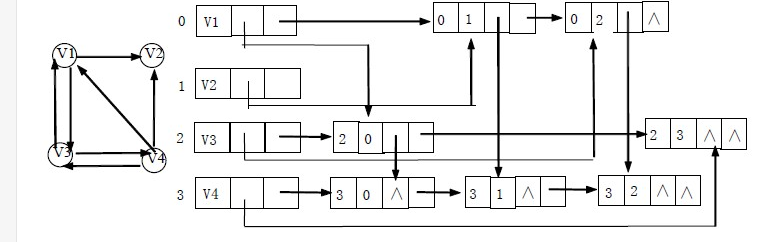
代码调试中的问题和解决过程

• 问题1：最大堆的代码实现
• 问题1解决方案：最大堆：堆中的最大元素存放在根节点的位置。
  除了根节点，其他每个节点的值最多与其父节点的值一样大。也就是任意一个子树中包含的所有节点的值都不大于树根节点的值。
  堆中节点的位置编号都是确定的，根节点编号为1，每一层从左到右依次编号。由堆是完全二叉树，可以知道当堆中某个节点的编号为i时，如果这个节点有左右子树，那么左子树的节点编号为2i,右子树的节点编号为2i+1（当然这是在根节点编号为1的情况时）。
  并且有n个节点的堆中叶子节点的编号为从n/2+1~n。因为假设节点n/2+1不是叶子节点，那么它的左子节点编号(n/2+1)2=n+1，而节点总共只有n个。完全二叉树的叶子节点只出现在最下面两层。最下层的叶子集中在左边，倒数二层的叶子集中在右边。
  维护最大堆函数MAX_HEAPWEIHU(A，i)，假定节点i的左右子树已经是最大堆。那么维护堆时，先比较i节点的值与左右节点值的大小，将三个数中的最大值交换到根节点的位置。假设根节点i与左子节点的值交换了，那么左子树就要再次调用MAX_HEAPWEIHU(A，2i)，判断左子树还是不是最大堆，如果是则结束，否则继续调用进行维护。因此调用MAX_HEAPWEIHU(A，i)的时间复杂度为O(logn)。
  代码实现：
  堆排序：（大根堆）

　　①将存放在array[0，...，n-1]中的n个元素建成初始堆；

　　②将堆顶元素与堆底元素进行交换，则序列的最大值即已放到正确的位置；

　　③但此时堆被破坏，将堆顶元素向下调整使其继续保持大根堆的性质，再重复第②③步，直到堆中仅剩下一个元素为止。

堆排序算法的性能分析：

　　空间复杂度:o(1)；

　　时间复杂度:建堆：o(n)，每次调整o(log n)，故最好、最坏、平均情况下：o(n*logn);

　　稳定性：不稳定
//构建大根堆：将array看成完全二叉树的顺序存储结构
private int[] buildMaxHeap(int[] array){
//从最后一个节点array.length-1的父节点（array.length-1-1）/2开始，直到根节点0，反复调整堆
for(int i=(array.length-2)/2;i>=0;i--){
adjustDownToUp(array, i,array.length);
}
return array;
}

//将元素array[k]自下往上逐步调整树形结构
private void adjustDownToUp(int[] array,int k,int length){
    int temp = array[k];   
    for(int i=2*k+1; i<length-1; i=2*i+1){    //i为初始化为节点k的左孩子，沿节点较大的子节点向下调整
        if(i<length && array[i]<array[i+1]){  //取节点较大的子节点的下标
            i++;   //如果节点的右孩子>左孩子，则取右孩子节点的下标
        }
        if(temp>=array[i]){  //根节点 >=左右子女中关键字较大者，调整结束
            break;
        }else{   //根节点 <左右子女中关键字较大者
            array[k] = array[i];  //将左右子结点中较大值array[i]调整到双亲节点上
            k = i; //【关键】修改k值，以便继续向下调整
        }
    }
    array[k] = temp;  //被调整的结点的值放人最终位置
}

然后进行堆排序：
//堆排序
public int[] heapSort(int[] array){
array = buildMaxHeap(array); //初始建堆，array[0]为第一趟值最大的元素
for(int i=array.length-1;i>1;i--){
int temp = array[0]; //将堆顶元素和堆低元素交换，即得到当前最大元素正确的排序位置
array[0] = array[i];
array[i] = temp;
adjustDownToUp(array, 0,i); //整理，将剩余的元素整理成堆
}
return array;
}

[代码托管]https://gitee.com/xingtianyue/events

（statistics.sh脚本的运行结果截图）

结对及互评

本周进行了关于关于查找和排序的补充实验，其中排序的补充实验和补充方法与20162313苑洪铭同学进行了讨论。

本周结对学习情况

- [结对同学学号1]https://home.cnblogs.com/u/yuanhongming/
- 结对照片
- 结对学习内容
    -关于堆排序以及堆和栈、树的对比
    - 图结构

xxx
xxx

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）	重要成长
目标	5000行	30篇	400小时
第一周	200/200	2/2	20/20
第二周	300/500	2/4	18/38
第三周	500/1000	3/7	22/60
第四周	300/1300	2/9	30/90

• 计划学习时间:16小时

• 实际学习时间:16小时