2017西安网络赛 计蒜客 Trig Function 切比雪夫多项式

http://www.docin.com/p-385138324.html 用以表示cosnx的关于cosx的多项式的通项公式

http://www.docin.com/p-232710665.html?docfrom=rrela 数列通项公式的求法(论文)

问答里说这个是切比雪夫多项式 我查了一下哇。。

第一类切比雪夫多项式

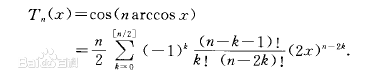
#include <stdio.h>
#include <cstring>
#include <iostream>
#include <math.h>
using namespace std;
#define LL long long
const int maxn=(int)1e5+5;
const LL MOD=998244353;
LL quickmod(LL a,LL b,LL m)
{
    LL r=1;
    while(b)
    {
        if(b&1)r=r*a%MOD;
        a=a*a%MOD;
        b>>=1;
    }
    return r;
}
int main()
{
#ifdef shuaishuai
    freopen("C:\Users\hasee\Desktop\a.txt","r",stdin);
    //freopen("C:\Users\hasee\Desktop\b.txt","w",stdout);
#endif
    LL n,m;
    int t;
    while(~scanf("%lld%lld",&n,&m))
    {
        LL a=0;
        if((n+m+1)%2) a=((n-m)/2)%2==0? 1:-1;
       // cout<<"a:"<<a<<endl;
        if(m>n||!a)
        {
            puts("0");
            continue;
        }
        if(m>=1){
            a=a*n%MOD;
            for(LL i=n+m-2; i>n-m; i-=2)
            {
                if(i==0) continue;
                a=a*i%MOD;
            }
        }
       // cout<<"a:"<<a<<endl;
        LL b=1;
        for(LL i=2; i<=m; i++)b=b*i%MOD;
        b=quickmod(b,MOD-2,MOD);
        cout<<(a*b%MOD+MOD)%MOD<<endl;

    }
    return 0;
}