数据结构和算法分析的编程习题。
(1)生成不重复的随机数,并且具有上界和下界。可以产生有序的,也可以产生无序的。
知识:
C编程语言不允许返回整个数组作为函数的参数。但是,您也可以返回一个指针,没有索引到一个数组中指定数组的名称。
例如:
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<time.h> 4 5 int *getRandom(){ 6 static int r[10]; 7 int i; 8 srand((unsigned)time(NULL)); 9 for ( i = 0; i < 10; ++i){ 10 r[i] = rand()%100; 11 printf( "r[%d] = %d ", i, r[i]); 12 } 13 return r; 14 } 15 16 int main(){ 17 int *p; 18 int i; 19 p= getRandom(); 20 for (i=0;i<10;i++){ 21 printf( "*(p+%d):%d ",i, *(p+i)); 22 } 23 return 0; 24 }
运行结果:

错误运用的实例:
1)在上述第6行,定义数组时未用static int r[10],而是int r[10],错误运行的结果如下:

从结果看,第一个是正确的,其余的值都已经无效。原因是,虽然返回的依然是数组的头指针,但由于数组是在函数中定义的,在函数运行结束后就会收回内存空间,导致错误。所以必须用static int r[10];
2)若定义r数组时没有指定固定数值的大小,而是通过参数动态指定:
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<time.h> 4 5 int *getRandom(int k,int h){ 6 //static int r[20-10];用这个不会出错,因为数组大小固定,编译时内存管理器能够预先分配好空间给静态数组 7 static int r[k-h];//这个是动态指定的,编译器无法预先分配内存空间,会出现错误 8 int i; 9 srand((unsigned)time(NULL)); 10 for ( i = 0; i < 10; ++i){ 11 r[i] = rand()%100; 12 printf( "r[%d] = %d ", i, r[i]); 13 } 14 return r; 15 } 16 17 int main(){ 18 int *p; 19 int i; 20 p= getRandom(20,10); 21 for (i=0;i<10;i++){ 22 printf( "*(p+%d):%d ",i, *(p+i)); 23 } 24 return 0; 25 }
则会出现下述错误:

解决方案:如果想要解决这个问题,则可以用malloc动态分配指定大小的内存空间:
#include<stdio.h> #include<stdlib.h> #include<time.h> int *getRandom(int k,int h){ //static int r[20-10];用这个不会出错,因为数组大小固定,编译时内存管理器能够预先分配好空间给静态数组 //static int r[k-h];//这个是动态指定的,编译器无法预先分配内存空间,会出现错误 int *r=(int *)malloc((k-h)*sizeof(int));//做这个例子时,文件后缀名是.cpp所以必须用强制类型转换 int i; srand((unsigned)time(NULL)); for ( i = 0; i < 10; ++i){ r[i] = rand()%100; printf( "r[%d] = %d ", i, r[i]); } return r; } int main(){ int *p; int i; p=getRandom(20,10); for (i=0;i<10;i++){ printf( "*(p+%d):%d ",i, *(p+i)); } return 0; }
本题答案:
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<time.h> 4 5 //随机数生成器 6 //生成从i到j范围内的总数为total的整数,不能重复且无顺序 7 int *RandInt4(int total,int i,int j,int order){ 8 int *numberGroup=malloc(total*sizeof(int));//用于返回一个指定大小的数组 9 int tempory[j-i+1];//辅助产生随机数的数组。 10 int k;//用于循环遍历 11 int x;//接收产生的随机变量 12 srand(time(NULL)); 13 //初始化辅助数组 14 for(k=0;k<=j-i;k++){ 15 tempory[k]=0; 16 } 17 for(k=0;k<total;k++){ 18 L: x=rand()%(j-i+1)+i;//产生从i到j,包括i和j的随机数 19 if(tempory[x-i]==0){ 20 tempory[x-i]=1; 21 //当需要产生的数组是无序的则执行: 22 if(order==0){ 23 numberGroup[k]=x; 24 } 25 }else{ 26 goto L; 27 } 28 } 29 //当需要产生有序的随机数组时执行: 30 int w=0; 31 if(order!=0){ 32 for(k=0;k<j-i+1;k++){ 33 if(tempory[k]==1){ 34 numberGroup[w++]=k+i; 35 if(w>=total){ 36 break; 37 } 38 } 39 } 40 } 41 42 return numberGroup; 43 } 44 //默认无序,生成从i到j的total个整数 45 int *RandInt3(int total,int i,int j){ 46 if(total<=j-i+1){ 47 return RandInt4(total,i,j,0); 48 }else{ 49 printf("生成的数组过大。 "); 50 exit(0); 51 } 52 } 53 //默认无序,生成从i到j的随机整数j-i+1个 54 int *RandInt2(int i,int j){ 55 return RandInt4(j-i+1,i,j,0); 56 } 57 int main(){ 58 int *a; 59 int k; 60 int total; 61 printf("下面测试这个函数的功能: "); 62 printf("产生20到39范围内有序的随机整数20个: "); 63 total=39-20+1; 64 a=RandInt4(total,20,39,1); 65 for(k=0;k<total;k++){ 66 printf("%3d",a[k]); 67 } 68 printf(" 产生15到34范围内无序的随机整数20个: "); 69 free(a); 70 total=34-15+1; 71 a=RandInt3(total,15,34); 72 for(k=0;k<total;k++){ 73 printf("%3d",a[k]); 74 } 75 printf(" 产生30~49范围内无序的随机整数: "); 76 free(a); 77 a=RandInt2(30,49); 78 total=49-30+1; 79 for(k=0;k<total;k++){ 80 printf("%3d",a[k]); 81 } 82 printf(" 产生30~49范围内有序的随机整数10个: "); 83 free(a); 84 total=10; 85 a=RandInt4(total,30,49,1); 86 for(k=0;k<total;k++){ 87 printf("%3d",a[k]); 88 } 89 free(a); 90 return 0; 91 }
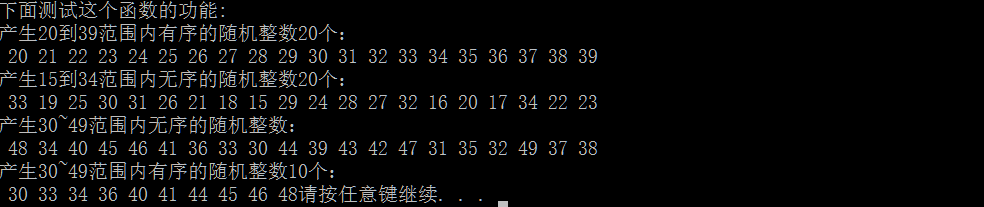
下面再给出另外两种算法:
1)算法1(更加低效):
生成随机数添入数组,当另外产生的随机数不同于所有的已经产生的随机数时才将新产生的随机数添入数组。
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<stdlib.h> 4 5 int exsist(int temp,int *p,int length){ 6 int i; 7 for(i=0;i<length;i++){ 8 if(temp==p[i]){ 9 return 1; 10 } 11 } 12 return 0; 13 } 14 int *RandInt(int i,int j){ 15 int x,k; 16 int *p=malloc((j-i)*sizeof(int)); 17 srand(time(NULL)); 18 for(k=0;k<j-i;k++){ 19 L: x=rand()%(j-i)+i; 20 if(!exsist(x,p,k)){ 21 p[k]=x; 22 }else{ 23 goto L; 24 } 25 } 26 return p; 27 } 28 int main(){ 29 int *p=RandInt(0,20); 30 int i; 31 for(i=0;i<20-0;i++){ 32 printf("%2d ",p[i]); 33 } 34 return 0; 35 }
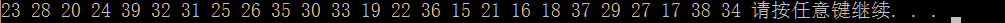
2)算法2:(更加高效):
在生成数到一个数组后,随机置换,打乱位置。
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<time.h> 4 5 int RandNumber(int k){ 6 int x=rand()%k; 7 return x; 8 } 9 void swap(int *a,int *b){ 10 int temp=*b; 11 *b=*a; 12 *a=temp; 13 } 14 int *RandInt(int i,int j){ 15 int *p=malloc(sizeof(int)*(j-i)); 16 int k; 17 for(k=0;k<j-i;k++){ 18 p[k]=i+k; 19 } 20 for(k=0;k<j-i;k++){ 21 swap(&p[k],&p[RandNumber(j-i)]); 22 } 23 return p; 24 } 25 int main(){ 26 srand(time(NULL)); 27 int i; 28 int *p=RandInt(20,40); 29 for(i=0;i<20;i++){ 30 printf("%d ",p[i]); 31 } 32 return 0; 33 }

(2)给出一个有效的算法确定在一个排序的数组中是否存在整数i使得Ai=i:
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<time.h> 4 5 int *RandInt4(int total,int i,int j,int order){ 6 int *numberGroup=malloc(total*sizeof(int));//用于返回一个指定大小的数组 7 int tempory[j-i+1];//辅助产生随机数的数组。 8 int k;//用于循环遍历 9 int x;//接收产生的随机变量 10 srand(time(NULL)); 11 //初始化辅助数组 12 for(k=0;k<=j-i;k++){ 13 tempory[k]=0; 14 } 15 for(k=0;k<total;k++){ 16 L: x=rand()%(j-i+1)+i;//产生从i到j,包括i和j的随机数 17 if(tempory[x-i]==0){ 18 tempory[x-i]=1; 19 //当需要产生的数组是无序的则执行: 20 if(order==0){ 21 numberGroup[k]=x; 22 } 23 }else{ 24 goto L; 25 } 26 } 27 //当需要产生有序的随机数组时执行: 28 int w=0; 29 if(order!=0){ 30 for(k=0;k<j-i+1;k++){ 31 if(tempory[k]==1){ 32 numberGroup[w++]=k+i; 33 if(w>=total){ 34 break; 35 } 36 } 37 } 38 } 39 return numberGroup; 40 } 41 void OldSearch(int *p,int length){ 42 int i; 43 for(i=0;i<length;i++){ 44 if(p[i]==i){ 45 printf("第%d个数是满足条件的,为%d ",i,p[i]); 46 } 47 } 48 } 49 void NewSearch(int *p,int low,int high){ 50 int i; 51 int mid=(low+high)/2; 52 if(high-low<2){ 53 if(low==p[low]){ 54 printf("第%d个数是满足条件的,为%d ",low,p[low]); 55 } 56 if(low!=high){ 57 if(high==p[high]){ 58 printf("第%d个数是满足条件的,为%d ",high,p[high]); 59 } 60 } 61 return; 62 } 63 if(mid<p[mid]){ 64 NewSearch(p,low,mid-1); 65 }else if(mid==p[mid]){ 66 NewSearch(p,low,mid-1); 67 printf("第%d个数满足条件的,为%d ",mid,p[mid]); 68 NewSearch(p,mid+1,high); 69 }else{ 70 NewSearch(p,mid+1,high); 71 } 72 } 73 int main(){ 74 int *p=RandInt4(30,-10,50,1); 75 int i; 76 for(i=0;i<30;i++){ 77 printf("第%2d个数是%2d",i,p[i]); 78 if((i+1)%5==0){ 79 printf(" "); 80 } 81 } 82 int n; 83 printf("请输入你想改变的位置: "); 84 scanf("%d",&n); 85 p[n]=n; 86 printf("用效率低的算法OldSearch: "); 87 OldSearch(p,30); 88 printf("用效率高的算法NewSearch: "); 89 NewSearch(p,0,29); 90 printf(" "); 91 }

(3)给出有效的算法:
1)求最小子序列和:
2)求最大的正子序列和:
3)求最大子序列乘积:
1 #include<stdio.h> 2 3 int MinSubSequenceSum(int *a,int length){ 4 int thisSum,minSum,k; 5 thisSum=minSum=0; 6 for(k=0;k<length;k++){ 7 thisSum+=a[k]; 8 if(thisSum<minSum){ 9 minSum=thisSum; 10 }else if(thisSum>0){ 11 thisSum=0; 12 } 13 } 14 return minSum; 15 } 16 int MinZSubSequenceSum(int *a,int length){ 17 int thisSum,minZSum,k; 18 thisSum=minZSum=0; 19 for(k=0;k<length;k++){ 20 if(a[k]>0){ 21 thisSum+=a[k]; 22 }else{ 23 thisSum=0; 24 } 25 if(thisSum>minZSum){ 26 minZSum=thisSum; 27 } 28 } 29 return minZSum; 30 } 31 int Sub(int *a,int begin,int end){ 32 int k; 33 long result=1; 34 for(k=begin;k<=end;k++){ 35 result=result*a[k]; 36 } 37 return result; 38 } 39 int MaxSubSequenceSub(int *a,int length){ 40 int n=0; 41 int k; 42 //负数出现的位置 43 int firstPosition,lastPosition; 44 firstPosition=0; 45 lastPosition=length; 46 //记录负数的个数 47 for(k=0;k<length;k++){ 48 if(a[k]<0){ 49 n++; 50 } 51 } 52 //记录第一次负数出现的位置 53 for(k=0;k<length;k++){ 54 if(a[k]<0){ 55 firstPosition=k; 56 break; 57 } 58 } 59 //记录最后一次负数出现的位置 60 for(k=length-1;k>=0;k--){ 61 if(a[k]<0){ 62 lastPosition=k; 63 break; 64 } 65 } 66 int sub1,sub2; 67 if(n%2==0){ 68 return Sub(a,0,length-1); 69 }else{ 70 sub1=Sub(a,0,lastPosition-1);//不能包括最后一个负数 71 sub2=Sub(a,firstPosition+1,length);//不能包括第一个负数 72 return sub1>sub2?sub1:sub2; 73 } 74 } 75 int main(){ 76 int a[]={ 77 -21,43,21,-32,-43,65,-67,-98,98,65 78 }; 79 printf("最小子序列和为%d ",MinSubSequenceSum(a,10)); 80 printf("最大正子序列和为%d ",MinZSubSequenceSum(a,10)); 81 printf("最大子序列乘积%d ",MaxSubSequenceSub(a,10)); 82 }

(4)编写一个程序确定一个数是否为素数,写出o(N),或根号N的程序:
1)算法1(高效算法):
1 #include<stdio.h> 2 #include<stdlib.h> 3 #define YI 1//不是素数 4 5 int main() 6 { 7 int m; 8 int bsss; 9 int pfg;//平方根 10 11 //输入处理 12 while(printf("请输入一个正整数:"),scanf("%d",&m)==0||m<0) 13 { 14 while(getchar()!=' ') ;//没有这句话,不符合%d格式的字符并没有被读取,而将一直存在于输入缓冲区 15 printf("输入不正确 "); 16 } 17 18 //处理几种特殊情况 19 { 20 if(m==2){ 21 printf("%d不是素数 ",m); 22 exit(1); 23 } 24 if(m==1||m%2==0){ 25 printf("%d不是素数 ",m); 26 exit(1); 27 } 28 } 29 ///求平方根的近似值,这里求的是最小的大于m平方根的整数 30 { 31 int m_=m,js; 32 for(pfg=1,js=1;m_>=0;pfg++,js+=2) 33 m_-=js; 34 } 35 36 ///判断大于2的奇数是不是素数 37 { 38 int i; 39 bsss=!YI; 40 for(i=3;i<pfg;i+=2) 41 { 42 if(m%i==0) 43 {bsss=!bsss; 44 break;} 45 } 46 } 47 printf("%d%s是素数 ",m,bsss==YI?"不":""); 48 return 0; 49 }
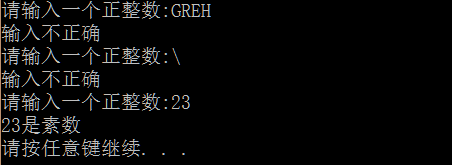
2)低效的算法
1 #include<stdio.h> 2 3 int IsPrime(int n){ 4 int i; 5 for(i=3;i<n/2+1;i=i+2){ 6 if(n%i==0){ 7 return 0; 8 } 9 } 10 return 1; 11 } 12 int main(){ 13 int n; 14 int x; 15 L: printf("请输入一个整数: "); 16 x=scanf("%d",&n); 17 while(getchar()!=' '); 18 if(x==0||x<0||n<0){ 19 printf("输入错误"); 20 goto L; 21 } 22 if(!IsPrime(n)){ 23 printf("%d不是素数 ",n); 24 }else{ 25 printf("%d是素数 ",n); 26 } 27 goto L; 28 }

(5)不用递归写出快速求幂的程序:
本题用斐波那契数列辅助求幂,当次方数较大时才会明显降低运算量。
算法原理:
如果要求一个数的n次幂,首先寻找与n相近的一个斐波那契数F,这个数小于等于n。则n次幂就等于F次幂再乘以(n-F)次幂。(n-F)次幂可以用递归来做,也可以用普通循环来做。而斐波那契数的次幂操作如下:
定义一个变量N记录此斐波那契数在数列中的位置,由于没有专门的函数,所以我们必须从n=1,f(n)=1开始进行f(N)=f(N-1)+f(N-2)的操作,一直到f(N)<=n,而f(N+1)>n。记下此时的N。然后做N次循环操作:i=1,result=x;i=2,result=x*x;i=3,result=x*(x*x);i=4,result=(x*x)*(x*x*x)......一直到i=N为止。result即为F次幂。
1 #include<stdio.h> 2 3 //普通求幂算法 4 unsigned long QiuMi(int x,int n){ 5 int i; 6 unsigned long result=1; 7 for(i=0;i<n;i++){ 8 result=result*x; 9 } 10 return result; 11 } 12 //利用斐波那契数快速求幂 13 unsigned long FB_QiuMi(int x,int n){ 14 if(n<=2){ 15 printf("不用求幂公式! "); 16 switch(n){ 17 case 1:return x; 18 case 2:return x*x; 19 } 20 } 21 //记录斐波那契数列的下标 22 int N=0; 23 int f=1; 24 int temp; 25 int flag=f+1; 26 while(flag<=n){ 27 temp=flag; 28 flag=flag+f; 29 f=temp; 30 N++; 31 } 32 int less=n-temp; 33 int i; 34 unsigned long result=x; 35 flag=x; 36 for(i=0;i<N;i++){ 37 temp=result; 38 result=result*flag; 39 flag=temp; 40 } 41 while(less>0){ 42 result=result*x; 43 less--; 44 } 45 return result; 46 } 47 int main(){ 48 printf("2的14次方为%ld ",QiuMi(2,10)); 49 printf("2的14次方为%ld ",FB_QiuMi(2,10)); 50 printf("2的20次方为%ld ",QiuMi(2,20)); 51 printf("2的20次方为%ld ",FB_QiuMi(2,20)); 52 printf("2的30次方为%ld ",QiuMi(2,30)); 53 printf("2的30次方为%ld ",FB_QiuMi(2,30)); 54 }

2)算法2:用公比为2的数列辅助求幂,与斐波那契数的类似,不过求数列的下标时有函数,可以直接用。用加权的方式来做:
例如:9二进制位1001,即是x的8次方乘以x的一次方。在程序中只需result=1后,result*a[4]*a[1]。其中a[4]=x^(2^(4-1)),a[1]=x^(2^(1-1))。a[n]=x^(2^(n-1))。
#include<stdio.h> #include<math.h> #define MAXN 1000 int PowersOfXO[MAXN]; int main() { int x, n, cnt, i; int ans = 1; printf("请输入x的值和它的次方数: "); scanf("%d %d", &x, &n); cnt = (int)log2(n); PowersOfXO[0] = x; for (i = 1; i <= cnt; i++){ PowersOfXO[i] = PowersOfXO[i - 1] * PowersOfXO[i - 1]; } i = 0; while (n > 0) {//将n转换为2进制,如果为1乘 if (n % 2 == 1) ans *= PowersOfXO[i]; i++; n /= 2; } printf("%d", ans); }

(6)大小为N的数组,其主要元素是一个出现次数超过N/2次数的元素,编写程序求主要元素。
1)普通的算法:
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<time.h> 4 5 void initNumberGroup(int *a,int length){ 6 int k; 7 for(k=0;k<length;k++){ 8 a[k]=rand()%3; 9 } 10 } 11 //判断数组中是否存在某个数 12 int exsist(int *p,int n,int x){ 13 int k; 14 for(k=0;k<n;k++){ 15 if(x==p[k]){ 16 return 1; 17 } 18 } 19 return 0; 20 } 21 int searchMainElement(int *a,int length){ 22 int p[5]; //存放a数组中不同种类的元素的一个集合 23 int q[5]; //存放对应的个数 24 int k,n=0; 25 for(k=0;k<length;k++){ 26 //如果在p数组中不存在a[k]这个元素 27 if(!exsist(p,n,a[k])){ 28 p[n++]=a[k]; 29 } 30 } 31 //初始化记录个数的数组 32 for(k=0;k<n;k++){ 33 q[k]=0; 34 } 35 int j; 36 for(k=0;k<length;k++){ 37 //对于数组a中的每个元素在p数组中都能找到一个值对应 38 for(j=0;j<n;j++){ 39 if(a[k]==p[j]){ 40 q[j]++; 41 break;//找到对应的位置就可以退出了 42 } 43 } 44 } 45 for(k=0;k<n;k++){ 46 printf("元素%d出现的次数为:%d ",p[k],q[k]); 47 } 48 for(k=0;k<n;k++){ 49 if(q[k]>=length/2){ 50 printf("这个数组的主要元素为%d ",p[k]); 51 } 52 } 53 } 54 int main(){ 55 srand(time(NULL)); 56 int a[40]; 57 int k; 58 initNumberGroup(a,40); 59 for(k=0;k<40;k++){ 60 printf("%2d",a[k]); 61 if((k+1)%10==0){ 62 printf(" "); 63 } 64 } 65 searchMainElement(a,40); 66 return 0; 67 }

2)高效的算法:(以后写!)
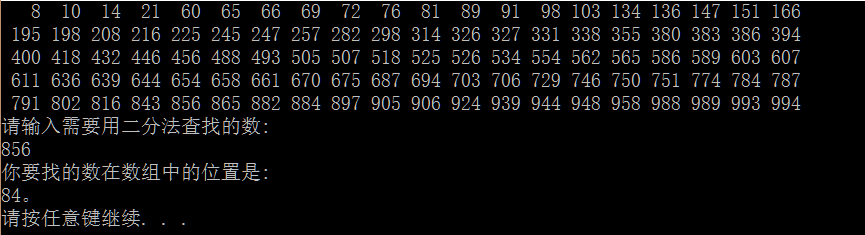
(7)实现对分查找算法,使得在每次迭代中只有一个二路比较:
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<time.h> 4 5 int BinarySearch(int a[],int x,int N){ 6 int Low,Mid,High; 7 Low=0;High=N-1; 8 while(Low<=High){ 9 Mid=(Low+High)/2; 10 if(a[Mid]<x){ //一路比较 11 Low=Mid+1; 12 }else{ 13 if(a[Mid]==x){ 14 return Mid; 15 } 16 High=Mid-1; 17 } 18 } 19 return -1; 20 } 21 int main(){ 22 srand((int)time(NULL)); 23 int i,x; 24 int a[1000],b[100];//数组a辅助产生不重复的随机数并排序 25 for(i=0;i<1000;i++){ 26 a[i]=0; 27 } 28 for(i=0;i<100;i++){ 29 //保证数组a中有99个数为1 30 L: x=rand()%1000; 31 if(a[x]==1){ 32 goto L; 33 }else{ 34 a[x]=1; 35 } 36 } 37 int j; 38 //随机产生的99个数放到数组b中 39 for(i=0,j=0;j<1000;j++){ 40 if(a[j]==1){ 41 b[i]=j; 42 i++; 43 }else{ 44 continue; 45 } 46 } 47 48 for(i=0;i<100;i++){ 49 printf("%4d",b[i]); 50 if((i+1)%20==0){ 51 printf(" "); 52 } 53 } 54 printf("请输入需要用二分法查找的数: "); 55 scanf("%d",&x); 56 printf("你要找的数在数组中的位置是: %d。 ", 57 BinarySearch(b,x,100)); 58 return 0; 59 }