http://codeforces.com/contest/1041/problem/F
题目大意:
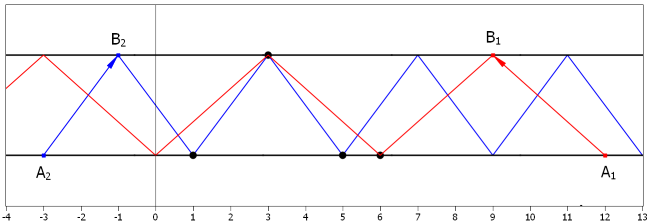
下边界有n个给定点,上边界有m个给定点,可以从任意一个点发出一条激光,激光碰到边界会反射
激光到达边界必须打到整数点,问最多可以打到几个给定点
输入格式:
第一行两个整数n,y1,表示下边界给定点的个数和下边界的纵坐标
第二行n个整数,表示给定点的横坐标
第三行两个整数m,y2,表示上边界给定点的个数和上边界的纵坐标
第四行m个整数,表示给定点的横坐标
题解:设起点横坐标为Xa,步长为Dx,则经过的第一行的点满足X=Xa+2*k*Dx,第二行的点满足X=Xa+(2*k+1)*Dx,发现步长为1时经过的点总可以覆盖步长Dx为奇数的点,所以可以通过步长为1来代替步长为奇数的情况,而当步长Dx为偶数时(即Dx=a*b,a为奇数,b为偶数),总可以转化成步长为b的情况,所以偶数都可以转化成步长为2的整数幂的情况,综上可得,只需要枚举2的0~29次幂即可,使用map存下来所有数%(2*Dx)的数量即可