通信网实验—Dijkstra算法

1 实验原理

Dijkstra（狄克斯特拉）算法用于计算通信网中指定节点到其他各节点的最短路径，简称D算法。Dijkstra算法的大致思路是，先把距离初始节点最近的节点找到，加入置定节点集( m{G_p})，再以这个节点为基础寻找下一个节点，每找到一个节点都加入到置定节点集( m{G_p})中，最终把初始节点到其他各个节点的最短距离依次找出。这里以节点1为初始节点说明：

• 构建一个距离（dis）列表，存入节点1到其他各个节点的距离。对于节点1不能直接到达的节点，则赋值为一个很大的数（比如999）代替；
• 从 dis 列表中，我们可以求得一个最小值，即是距离初始节点 1 最近的一个点，我们假设是节点 3。这也是从节点 1 到节点 3 的最短路径，因为无论从初始节点经过别的任何节点再到节点 3 的距离肯定大于这个最小值，这时把节点3存入置定节点集( m{G_p});
• 接下来更新 dis 列表，即比较初始节点 1 到其它各个节点的距离与节点 1 经过节点 3 再到其它节点的距离，保存较小的那一个值存入 dis 列表。再找出新的 dis 列表里面，除了确定点之外的最小的值，即是下一个要确定的点;
• 依次执行上述步骤，直到每一个点都确定，此时 dis 列表中所存的数据既 是初始节点到其它各个节点的最短距离。

2 实验仿真

通过Python实现Dijkstra算法的函数Dijkstra (D, begin, end)，其中：

• D为输入的无向图节点间路径长度矩阵；
• begin为起始节点；
• end为目标节点。

例题中的无向图有6个节点，如下图所示：

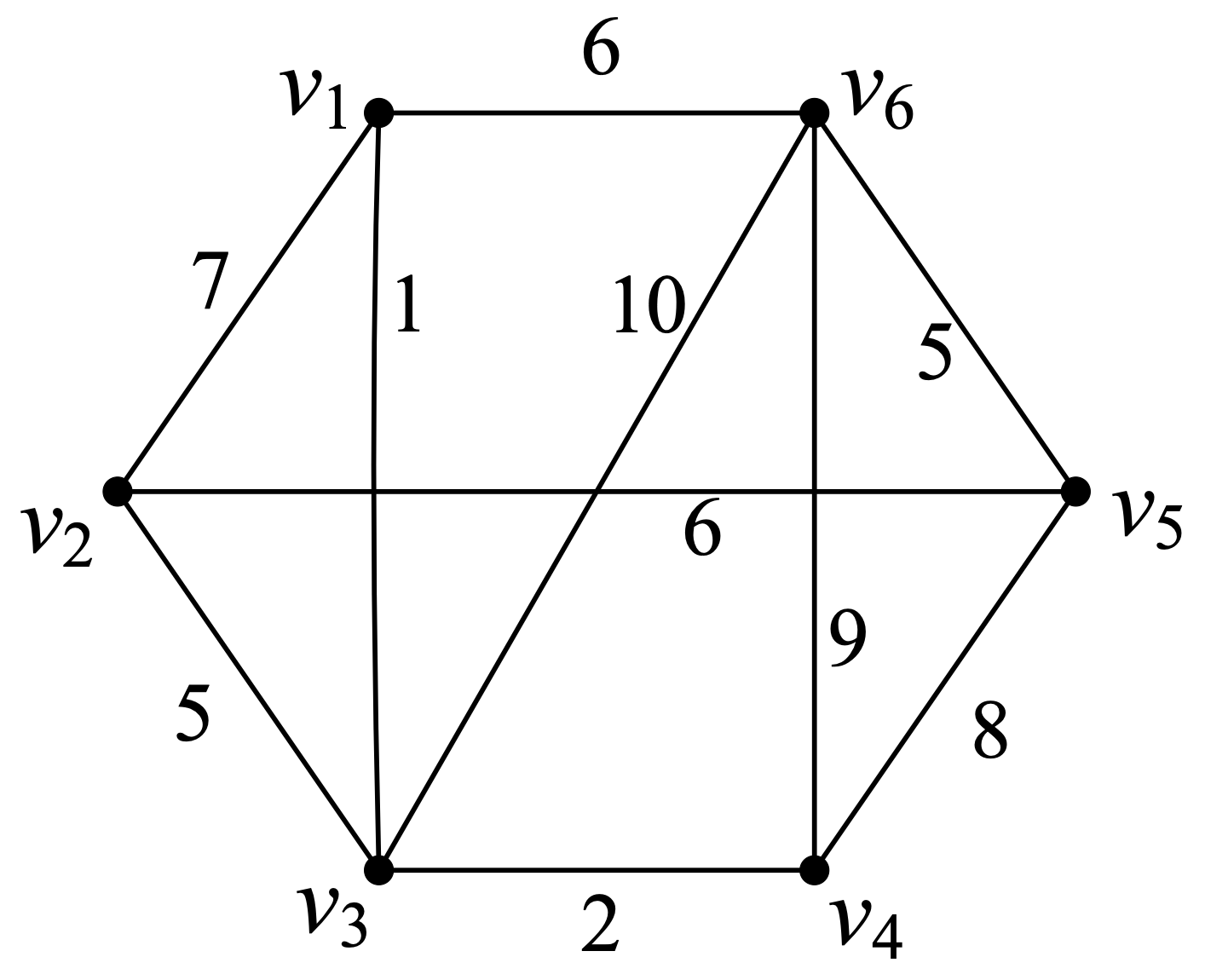
根据无向图可以得到节点间的距离矩阵可表示为：

[left[egin{array}{cccccc} 0 & 7 & 1 & infty & infty & 6 \ 7 & 0 & 5 & infty & 6 & infty \ 1 & 5 & 0 & 2 & infty & 10 \ infty & infty & 2 & 0 & 8 & 9 \ infty & 6 & infty & 8 & 0 & 5 \ 6 & infty & 10 & 9 & 5 & 0 end{array} ight] ]

假定初始节点为节点1，目标节点为节点5，则最短路径以及径长的仿真结果如下所示：

3 代码

'''
Created on 2020.10.30
@auther: Maye Zhang
'''
# D为输入的距离矩阵
# begin、end分别为起始点和终止点
def Dijkstra(D, begin, end):
    Dis = D[begin - 1]  #需要迭代更新的表

    print('初始化:', end='')
    print(Dis)

    path = [0] * len(Dis)   #存储到这个节点前最后一个经过的节点
    # 需要依次更新表
    for i in range(1, len(Dis)):
        # 难点在需要找到第i个最小值的索引，注意碰到最小值相同时怎么找索引
        a = [(key, value) for key, value in enumerate(Dis)]
        mid = sorted(a, key=lambda x: x[1])[i]  #确定第i个点
        mid_index = mid[0]
        mid_value = mid[1]

        print('确定第{}个点:'.format(mid_index+1), end='')
        print(Dis)
        # 更新Dis表
        # Dis = [min(Dis[k], mid_value + D[mid_index][k]) for k in range(len(Dis))]
        for k in range(len(Dis)):
            if mid_value + D[mid_index][k] < Dis[k]:
                Dis[k] = mid_value + D[mid_index][k]
                path[k] = mid_index + 1     #更新路径，保存更新的中间节点
        # 如果最小节点找到了目的节点，可以直接退出
        if mid_index + 1 == end:
            break
    # https://blog.csdn.net/jinixin/article/details/52247763
    value = end
    node_list = []
    for _ in range(len(Dis)):
        value = path[value - 1]
        if value != 0:
            node_list.append(value)
        else:
            break
    node_list.append(begin)
    node_list.reverse()
    node_list.append(end)

    node_list = list(map(str, node_list))
    print('最短径长为{0},最短路径为:'.format(Dis[end-1]), end='')
    print('->'.join(node_list))

检验：

inf = 999

# 距离矩阵
D = [
    [0, 7, 1, inf, inf, 6],
    [7, 0, 5, inf, 6, inf],
    [1, 5, 0, 2, inf, 10],
    [inf, inf, 2, 0, 8, 9],
    [inf, 6, inf, 8, 0, 5],
    [6, inf, 10, 9, 5, 0]
]

Dijkstra(D, 1, 5)