3.4 空间滤波基础
• Images are often corrupted by random variations in intensity, illumination, or have poor contrast and can’t be used directly.
• Filtering: transform pixel intensity values to reveal certain image characteristics
– Enhancement: improves contrast – Smoothing: remove noises – Template matching: detects known patterns.
空间滤波器由一个邻域(典型是个小矩形)及其所涵盖的图像像素执行预定义操作组成。 滤波产生的新像素坐标等于邻域中心的坐标。滤波(filtering)一词是借用频域处理中的词汇,是指接受或者拒绝一定的频率分量,。 例如,通过低频的滤波器称为低通滤波器。
What is a mask
A mask is a filter. Concept of masking is also known as spatial filtering. Masking is also known as filtering. In this concept we just deal with the filtering operation that is performed directly on the image.
-masking 是 指在image 领域的 filtering。
What is filtering
The process of filtering is also known as convolving a mask with an image. As this process is same of convolution so filter masks are also known as convolution masks.
-filtering 是 mask 与 image 进行卷积操作,所以mask 又叫 卷积掩膜。
总结:filtering 是信号邻域的词汇,用来消除随机产生的噪声或者加强信号的特点。 当传到digital image processing(DIP)领域以后,也可以叫masking。 而滤波也好,masking 也罢,本质上都是卷积操作,或者是相关操作。
3.4.1 空间滤波机理
- 如果在图像像素上执行线性操作,那该滤波器称为线性滤波器
- 否则称为非线性滤波器

空间滤波的机理示于图3.32。该处理就是在待处理图像中逐点地移动掩模。在每一点(x,y)处,滤波器在该点的响应通过事先定义的关系来计算。对于线性空间滤波(见2.6节线性的定义),其响应由滤波器系数与滤波掩模扫过区域的相应像索值的乘积之和给出。 图3.32所示为3×3的掩模,在图像中的点(x,y)处,用该掩模线性滤波的响应R为:
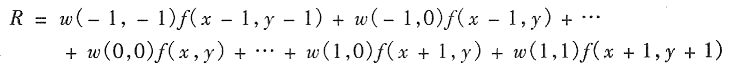
我们看到的是掩模系数与直接在掩模下的相应像素的乘积之和。注意,具体地说,系数ω(0,0)与图像值f(x,y)相符合是指当乘积求和计算发生时,掩模位于(x,y)的中心。对于一个尺寸为m×n的掩模,我们假设m=2a十1且n=2b+l,这里a,b为非负整数。即,在后续的讨论中,处理的掩模的长与宽都为奇数,其有意义的最小尺寸3×3(在我们的讨论中排除了无足轻重的1×1掩模)。
一般来说,在M×N的图像f上,用m×n大小的滤波器掩模进行线性滤波由下式给出:

3.4.2 空间相关(Correlation)与卷积(Convolution)操作
一维:
为了便于理解,我们先引入一维函数滤波的概念,再引入二维图像的滤波。基本原理:滤波器w与函数f起始位置对齐后,逐位移动,并且每次移动都进行按位相乘结果累加得到某位的结输出。设,一维函数 f 为: 0 0 0 0 1 0 0 0 0 ; 滤波器 w:1 2 3 4 5相关运算的过程:1、对齐:将 w 的开始位置 5 与 f 的开始位置 0对齐。对齐位置作为运算起点。2、填充:为了使得 w 每一次运算中各位都有值相乘,对 f 起始位置和结尾无对应位的位置进行“0填充”。(注意下填充的概念,在图像滤波中,填充的值对图像滤波的影响比较大。)。3、 计算:将上下对应的位相乘后全部相加得到结果的第一位,输出位置总是在。向右移动滤波器w “N”位,并进行相同的运算得到相应第N位的计算结果。4、 输出大小: Matlab中我们使用imfilter函数来进行卷积或者相关运算;(后文中,将具体介绍imfilter函数。)得到的结果的大小分为“full”和“same”两类,full包含填充项,same为原f大小。
二维:
一维和二维的情况很相像,需要注意填充扩展对图像的影响,我们将在后面的实验中讨论。总的来说:从开始位置平移掩膜到第一行运行结束位置,在每个位置上执行掩膜覆盖的亮度值与对应的掩膜系数相乘结果累加得到对应点的像素值。然后跳到第二行的起始位置继续平移和运算,如此反复直到掩膜移动到 整个运算的结束位置。(不过根据设定输出图像大小为same还是full,掩膜移动的范围有所不同。后文将讲具体描述。)关于掩膜的大小:通常使用奇数维的方阵作为掩膜/滤波器,因为奇数维的方正有唯一的一个中心点,比较直观。相关运算:1、对齐:得到same大小的输出结果,只需要保证掩膜中心能够覆盖全图每个像素点即可。此时只需将掩膜中心与图像矩阵第一行第一个元素对齐即可。full 的情况如下图,得到的有值的区域可能会有所拓宽,不过不影响原图大小尺寸的滤波结果的得出。2、填充:同一维中的理由,在二维中我们需要对图像进行填充。Matlab中的填充方式有4种:a/ 通过值P来进行扩展。(P为常量值,如本例中使用的为“0”)
b/ 过复制图像边界进行扩展填充。
c/ 过镜像反射图像边界来扩展填充。d/ 图像看成二维周期函数来扩展。在函数imfilter中会有具体的参数来设置这几种方式。后面函数介绍部分会具体描述。3、运算:将掩膜覆盖的亮度值与对应的掩膜系数相乘后结果累加得到对应点的输出像素值。然后进行平移继续运算,如此反复,直到平移结束位置。4、输出大小:分为full 类型和same类型。其意义与一维中一致。卷积运算的情况与相关类似,不过对掩膜进行了180°的旋转。
公式表示:w表示模板,f表示图像
 |
 |
| 模板 mask | 图像 |
注:(s,t)指的是该点距离当前中心像素点的相对位置
上面的公式是表示相关,应该用空心的五角星,但是没找到。 w和f是对应位置相乘。
上面的公式表示卷积,是实心的五角星。 w和f的转置的对应位置相乘。
3.4.3 线性滤波器的向量表示
3.4.4 空间滤波器的模板的产生
生成一个大小为m*n的线性空间滤波器要求制定mn个模板系数,这些系数是根据所要求的操作得到的。例如,我们想把图像中的像值替换为以这些点为中心点的,3*3的领域的平局灰度代替。 就出现了平均模板:
在某些应用中,我们有一个具有两个变量的连续函数,其目的是得到一个空间滤波模板。例如:有两个变量的高斯函数的基本形式如下:
delte是标准差,控制二维高斯函数钟形的“紧度”。通常我们设坐标x,y是整数(图像的像素坐标),如果想用这个二元函数生成3*3的模板,那么就关于其中心进行取样。
这样,就有。 如下图所示:

3.5 平滑空间滤波器
平滑线性滤波器,也叫均值滤波器,是低通滤波器( 因为这样的操作降低了灰度的‘尖锐’变化)
- 所有系数都相等的滤波器,可以看出是求模板内像素的平均值
- 加权平均模板,根绝不同位置设定不同权重,如下图,权重随距离增加递减。对角线位置距离比直接接触的距离大,所以权重变为1。按照1/2的等比随着距离增加进行递减。重要:这个模板的目的是 在平滑处理中降低模糊

统计排序(非线性)滤波器
以滤波器包围的图像区域中包含的像素的排序为基础,然后使用统计排序结果决定代替中心的像素值。最知名的叫 中值滤波器,这种滤波器对脉冲噪声非常有效,也称为椒盐噪声。
分析: 因为滤波器用统计中的数列中值代替模板中心位置处的值,这样就比均值更加保证了锐度的特点。使得拥有不同灰度的点看起来更接近于它的相邻点。
注:既然是统计特性决定的输出,可以取50%处的值,也可以取最小值,最大值等等其他的统计特性。


===========补充阅读
1. In image processing, a kernel, convolution matrix, or mask is a small matrix useful for blurring, sharpening, embossing, edge-detection, and more. This is accomplished by means of convolution between a kernel and an image.
2. Image Filtering in the Spatial Domain。
Filtering is a technique for modifying or enhancing an image. For example, you can filter an image to emphasize certain features or remove other features. Image processing operations implemented with filtering include smoothing, sharpening, and edge enhancement.
Filtering is a neighborhood operation, in which the value of any given pixel in the output image is determined by applying some algorithm to the values of the pixels in the neighborhood of the corresponding input pixel. A pixel's neighborhood is some set of pixels, defined by their locations relative to that pixel. (SeeNeighborhood or Block Processing: An Overview for a general discussion of neighborhood operations.) Linear filtering is filtering in which the value of an output pixel is a linear combination of the values of the pixels in the input pixel's neighborhood.



