网络流算法小结（转）

转自：http://dantvt.is-programmer.com/posts/7974.html

通过 USACO 4.2.1 Ditch 学习一下最大流算法 。可惜它给的测试数据几乎没有任何杀伤力，后面测试时我们采用 DD_engi 写的程序生成的加强版数据。

总体上来说，最大流算法分为两大类：增广路 (Augmenting Path) 和预流推进重标号 (Push Relabel)。也有算法同时借鉴了两者的长处，如 Improved SAP。本篇主要介绍增广路类算法，思想、复杂度及实际运行效率比较，并试图从中选择一种兼顾代码复杂度和运行效率的较好方案。以下我们将会看到，有时理论分析的时间复杂度并不能很好的反映一种算法的实际效率。

1. Ford - Fulkerson 方法

所有增广路算法的基础都是 Ford - Fulkerson 方法。称之为方法而不是算法是因为 Ford - Fulkerson 只提供了一类思想，在此之上的具体操作可有不同的实现方案。

给定一个有向网络 G(V,E) 以及源点 s 终点 t ，FF 方法描述如下：

Ford-Fulkerson 方法 (G,s,t)
1 将各边上流量 f 初始化为 0
2 while 存在一条增广路径 p
3     do 沿路径 p 增广流量 f
4 return f

假设有向网络 G 中边 (i,j) 的容量为 c(i,j) ，当前流量为 f(i,j) ，则此边的剩余流量即为 r(i,j) = c(i,j) - f(i,j) ，其反向边的剩余流量为 r(j,i) = f(i,j) 。有向网中所有剩余流量 r(i,j) > 0 的边构成残量网络 G_f ，增广路径 p 即是残量网络中从源点 s 到终点 t 的路径。

沿路径 p 增广流量f的操作基本都是相同的，各算法的区别就在于寻找增广路径 p 的方法不同。例如可以寻找从 s 到 t 的最短路径，或者流量最大的路径。

2. Edmonds - Karp 算法

Shortest Augmenting Path (SAP) 是每次寻找最短增广路的一类算法，Edmonds - Karp 算法以及后来著名的 Dinic 算法都属于此。SAP 类算法可统一描述如下：

Shortest Augmenting Path
1 x <-- 0
2 while 在残量网络 G_x 中存在增广路 s ~> t
3     do 找一条最短的增广路径 P
4        delta <-- min{r_ij:(i,j) 属于 P}
5        沿 P 增广 delta 大小的流量
6        更新残量网络 G_x
7 return x

在无权边的有向图中寻找最短路，最简单的方法就是广度优先搜索 (BFS)，E-K 算法就直接来源于此。每次用一遍 BFS 寻找从源点 s 到终点 t 的最短路作为增广路径，然后增广流量 f 并修改残量网络，直到不存在新的增广路径。

E-K 算法的时间复杂度为 O(VE²)，由于 BFS 要搜索全部小于最短距离的分支路径之后才能找到终点，因此可以想象频繁的 BFS 效率是比较低的。实践中此算法使用的机会较少。

3. Dinic 算法

BFS 寻找终点太慢，而 DFS 又不能保证找到最短路径。1970年 Dinic 提出一种思想，结合了 BFS 与 DFS 的优势，采用构造分层网络的方法可以较快找到最短增广路，此算法又称为阻塞流算法 (Blocking FlowAlgorithm)。

首先定义分层网络 AN(f)。在残量网络中从源点 s 起始进行 BFS，这样每个顶点在 BFS 树中会得到一个距源点 s 的距离 d，如 d(s) = 0，直接从 s 出发可到达的点距离为 1，下一层距离为2 ... 。称所有具有相同距离的顶点位于同一层，在分层网络中，只保留满足条件 d(i) + 1 = d(j) 的边，这样在分层网络中的任意路径就成为到达此顶点的最短路径。

Dinic 算法每次用一遍 BFS 构建分层网络 AN(f)，然后在 AN(f) 中一遍 DFS 找到所有到终点 t 的路径增广；之后重新构造 AN(f)，若终点 t 不在 AN(f) 中则算法结束。DFS 部分算法可描述如下：

 1 p <-- s
 2 while s 的出度 > 0 do
 3     u <-- p.top
 4     if u != t then
 5         if u 的出度 > 0 then
 6             设 (u,v) 为 AN(f) 中一条边
 7             p <-- p, v
 8         else
 9             从 p 和 AN(f) 中删除点 u 以及和 u 连接的所有边
10     else
11         沿 p 增广
12         令 p.top 为从 s 沿 p 可到达的最后顶点
13 end while

 

 实际代码中不必真的用一个图来存储分层网络，只需保存每个顶点的距离标号并在 DFS 时判断 dist[i] + 1 = dist[j] 即可。Dinic 的时间复杂度为 O(V²E)。由于较少的代码量和不错的运行效率，Dinic 在实践中比较常用。具体代码可参考 DD_engi 网络流算法评测包中的标程，这几天 dinic 算法的实现一共看过和比较过将近 10 个版本了，DD 写的那个在效率上是数一数二的，逻辑上也比较清晰。

 4. Improved SAP 算法

 本次介绍的重头戏。通常的 SAP 类算法在寻找增广路时总要先进行 BFS，BFS 的最坏情况下复杂度为 O(E)，这样使得普通 SAP 类算法最坏情况下时间复杂度达到了 O(VE²)。为了避免这种情况，Ahuja 和 Orlin 在1987年提出了Improved SAP 算法，它充分利用了距离标号的作用，每次发现顶点无出弧时不是像 Dinic 算法那样到最后进行 BFS，而是就地对顶点距离重标号，这样相当于在遍历的同时顺便构建了新的分层网络，每轮寻找之间不必再插入全图的 BFS 操作，极大提高了运行效率。国内一般把这个算法称为 SAP...显然这是不准确的，毕竟从字面意思上来看 E-K 和 Dinic 都属于 SAP，我还是习惯称为 ISAP 或改进的 SAP 算法。

 与 Dinic 算法不同，ISAP 中的距离标号是每个顶点到达终点 t 的距离。同样也不需显式构造分层网络，只要保存每个顶点的距离标号即可。程序开始时用一个反向 BFS 初始化所有顶点的距离标号，之后从源点开始，进行如下三种操作：(1)当前顶点 i 为终点时增广 (2) 当前顶点有满足 dist[i] = dist[j] + 1 的出弧时前进 (3) 当前顶点无满足条件的出弧时重标号并回退一步。整个循环当源点 s 的距离标号 dist[s] >= n 时结束。对 i 点的重标号操作可概括为 dist[i] = 1 + min{dist[j] : (i,j)属于残量网络G_f}。具体算法描述如下：

algorithm Improved-Shortest-Augmenting-Path
 1 f <-- 0
 2 从终点 t 开始进行一遍反向 BFS 求得所有顶点的起始距离标号 d(i)
 3 i <-- s
 4 while d(s) < n do
 5     if i = t then    // 找到增广路
 6         Augment
 7         i <-- s      // 从源点 s 开始下次寻找
 8     if G_f 包含从 i 出发的一条允许弧 (i,j)
 9         then Advance(i)
10         else Retreat(i)    // 没有从 i 出发的允许弧则回退
11 return f

procedure Advance(i)
1 设 (i,j) 为从 i 出发的一条允许弧
2 pi(j) <-- i    // 保存一条反向路径，为回退时准备
3 i <-- j        // 前进一步，使 j 成为当前结点

procedure Retreat(i)
1 d(i) <-- 1 + min{d(j):(i,j)属于残量网络G_f}    // 称为重标号的操作
2 if i != s
3     then i <-- pi(i)    // 回退一步

procedure Augment
1 pi 中记录为当前找到的增广路 P
2 delta <-- min{r_ij:(i,j)属于P}
3 沿路径 P 增广 delta 的流量
4 更新残量网络 G_f

 

 算法中的允许弧是指在残量网络中满足 dist[i] = dist[j] + 1 的弧。Retreat 过程中若从 i 出发没有弧属于残量网络 G_f 则把顶点距离重标号为 n 。

 虽然 ISAP 算法时间复杂度与 Dinic 相同都是 O(V²E)，但在实际表现中要好得多。要提的一点是关于 ISAP 的一个所谓 GAP 优化。由于从 s 到 t 的一条最短路径的顶点距离标号单调递减，且相邻顶点标号差严格等于1，因此可以预见如果在当前网络中距离标号为 k (0 <= k < n) 的顶点数为 0，那么可以知道一定不存在一条从 s 到 t 的增广路径，此时可直接跳出主循环。在我的实测中，这个优化是绝对不能少的，一方面可以提高速度，另外可增强 ISAP 算法时间上的稳定性，不然某些情况下 ISAP 会出奇的费时，而且大大慢于 Dinic 算法。相对的，初始的一遍 BFS 却是可有可无，因为 ISAP 可在循环中自动建立起分层网络。实测加不加 BFS 运行时间差只有 5% 左右，代码量可节省 15~20 行。

 5. 最大容量路径算法 (Maximum Capacity Path Algorithm)

 1972年还是那个 E-K 组合提出的另一种最大流算法。每次寻找增广路径时不找最短路径，而找容量最大的。可以预见，此方法与 SAP 类算法相比可更快逼近最大流，从而降低增广操作的次数。实际算法也很简单，只用把前面 E-K 算法的 BFS 部分替换为一个类 Dijkstra 算法即可。USACO 4.2 节的说明详细介绍了此算法，这里就不详述了。

 时间复杂度方面。BFS 是 O(E)，简单 Dijkstra 是 O(V²)，因此效果可想而知。但提到 Dijkstra 就不能不提那个 Heap 优化，虽然 USACO 的算法例子中没有用 Heap ，我自己还是实现了一个加 Heap 的版本，毕竟 STL 的优先队列太好用了不加白不加啊。效果也是非常明显的，但比起 Dinic 或 ISAP 仍然存在海量差距，这里就不再详细介绍了。

 6. Capacity Scaling Algorithm

 不知道怎么翻比较好，索性就这么放着吧。叫什么的都有，容量缩放算法、容量变尺度算法等，反正就那个意思。类似于二分查找的思想，寻找增广路时不必非要局限于寻找最大容量，而是找到一个可接受的较大值即可，一方面有效降低寻找增广路时的复杂度，另一方面增广操作次数也不会增加太多。时间复杂度 O(E²logU) 实际效率嘛大约稍好于最前面 BFS 的 E-K 算法，稀疏图时表现较优，但仍然不敌 Dinic 与 ISAP。

 7. 算法效率实测！

 重头戏之二，虽然引用比较多，哎~

 首先引用此篇强文 《Maximum Flow: Augmenting Path Algorithms Comparison》

 对以上算法在稀疏图、中等稠密图及稠密图上分别进行了对比测试。直接看结果吧：

稀疏图：

ISAP 轻松拿下第一的位置，图中最左边的 SAP 应该指的是 E-K 算法，这里没有比较 Dinic 算法是个小遗憾吧，他把 Dinic 与 SAP 归为一类了。最大流量路径的简单 Dijkstra 实现实在是太失败了 - -，好在 Heap 优化后还比较能接受……可以看到 Scaling 算法也有不错的表现。

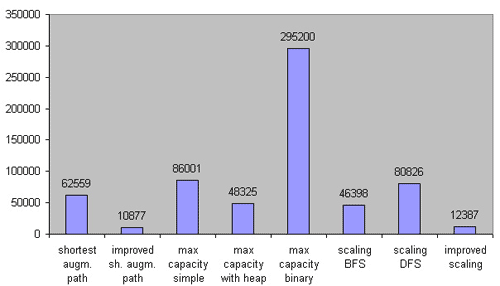
 中等稠密图：

 

 ISAP 依然领先。最大流量算法依然不太好过……几个 Scaling 类算法仍然可接受。

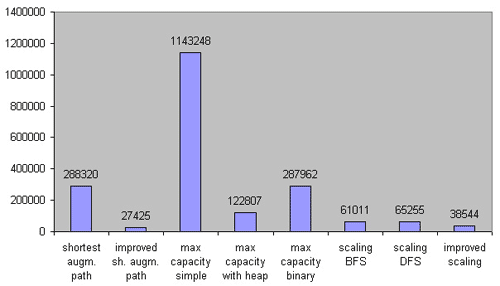
 稠密图：

 

 ISAP……你无敌了！这次可以看出 BFS 的 Scaling 比 DFS 实现好得多，而且几乎与 Improved Scaling 不相上下，代码量却差不少。看来除 ISAP 外 BFS Scaling 也是个不错的选择。

 最后补个我自己实测的图，比较算法有很多是 DD 网络流算法评测包里的标程，评测系统用的 Cena，评测数据为 DD ditch 数据生成程序生成的加强版数据：

 

 我一共写了 7 个版本的 ISAP ，Dinic 算法也写了几个递归版的但效率都不高，只放上来一个算了。从上图来看似乎 ISAP 全面超越了号称最大流最快速算法的 HLPP，但在另外一台机器上测试结果与此却不大相同，有时 ISAP 与 HLPP 基本持平，有时又稍稍慢一些。在这种差距非常小的情况下似乎编译器的效果也比较明显。那个 HLPP 是用 PASCAL 写的，我不知在 Win32 平台下编译代码效率如何，至少我的几个 ISAP 用 VC2008 + SP1 编译比用 g++ 要强不少，也可能是参数设置的问题。

不过这些都是小事，关键是见证了 ISAP 的实际效率。从上面可以看出不加 GAP 优化的 ISAP 有几个测试点干脆无法通过，而不加 BFS 却无甚大影响，递归与非递归相差在 7% 左右的样子。综合以上表现，推荐采用 ISAP 不加 BFS，非递归 + GAP 优化的写法，Ditch 这道题一共也才 80 行左右代码。要提的一点是 GAP 优化用递归来表现的话不如 while 循环来得直接。另外，看起来 HLPP 表现确实很优秀，有机会也好好研究一下吧，预流推进重标号算法也是一大类呢……

最后附上一个 ISAP + GAP + BFS 的非递归版本代码，网络采用邻接表 + 反向弧指针：

#include<cstdio>
#include<memory>

using namespace std;

const int maxnode = 1024;
const int infinity = 2100000000;

struct edge{
    int ver;    // vertex
    int cap;    // capacity
    int flow;   // current flow in this arc
    edge *next; // next arc
    edge *rev;  // reverse arc
    edge(){}
    edge(int Vertex, int Capacity, edge *Next)
        :ver(Vertex), cap(Capacity), flow(0), next(Next), rev((edge*)NULL){}
    void* operator new(size_t, void *p){
        return p;
    }
}*Net[maxnode];
int dist[maxnode]= {0}, numbs[maxnode] = {0}, src, des, n;

void rev_BFS(){
    int Q[maxnode], head = 0, tail = 0;
    for(int i=1; i<=n; ++i){
        dist[i] = maxnode;
        numbs[i] = 0;
    }

    Q[tail++] = des;
    dist[des] = 0;
    numbs[0] = 1;
    while(head != tail){
        int v = Q[head++];
        for(edge *e = Net[v]; e; e = e->next){
            if(e->rev->cap == 0 || dist[e->ver] < maxnode)continue;
            dist[e->ver] = dist[v] + 1;
            ++numbs[dist[e->ver]];
            Q[tail++] = e->ver;
        }
    }
}

int maxflow(){
    int u, totalflow = 0;
    edge *CurEdge[maxnode], *revpath[maxnode];
    for(int i=1; i<=n; ++i)CurEdge[i] = Net[i];
    u = src;
    while(dist[src] < n){
        if(u == des){    // find an augmenting path
            int augflow = infinity;
            for(int i = src; i != des; i = CurEdge[i]->ver)
                augflow = min(augflow, CurEdge[i]->cap);
            for(int i = src; i != des; i = CurEdge[i]->ver){
                CurEdge[i]->cap -= augflow;
                CurEdge[i]->rev->cap += augflow;
                CurEdge[i]->flow += augflow;
                CurEdge[i]->rev->flow -= augflow;
            }
            totalflow += augflow;
            u = src;
        }
 
        edge *e;
        for(e = CurEdge[u]; e; e = e->next)
            if(e->cap > 0 && dist[u] == dist[e->ver] + 1)break;
        if(e){    // find an admissible arc, then Advance
            CurEdge[u] = e;
            revpath[e->ver] = e->rev;
            u = e->ver;
        } else {    // no admissible arc, then relabel this vertex
            if(0 == (--numbs[dist[u]]))break;    // GAP cut, Important!
            CurEdge[u] = Net[u];
            int mindist = n;
            for(edge *te = Net[u]; te; te = te->next)
                if(te->cap > 0)mindist = min(mindist, dist[te->ver]);
            dist[u] = mindist + 1;
            ++numbs[dist[u]];
            if(u != src)
                u = revpath[u]->ver;    // Backtrack
        }
    }
    return totalflow;
}
 
int main(){
    int m, u, v, w;
    freopen("ditch.in", "r", stdin);
    freopen("ditch.out", "w", stdout);
    while(scanf("%d%d", &m, &n) != EOF){    // POJ 1273 need this while loop
        edge *buffer = new edge[2*m];
        edge *data = buffer;
        src = 1; des = n;

        while(m--){
            scanf("%d%d%d", &u, &v, &w);
            Net[u] = new((void*) data++) edge(v, w, Net[u]);
            Net[v] = new((void*) data++) edge(u, 0, Net[v]);
            Net[u]->rev = Net[v];
            Net[v]->rev = Net[u];
        }
        rev_BFS();
        printf("%d
", maxflow());
        delete [] buffer;
    }
    return 0;
}