【bzoj2875】 Noi2012—随机数生成器

http://www.lydsy.com/JudgeOnline/problem.php?id=2875 (题目链接)

题意

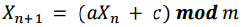　　求${X_{n}}$。

Solution

　　矩乘板子，这里主要讲下会爆long long的整数相乘取模，我们用double可以做到${O(1)}$。

　　求${(AB)~mod~C}$。求出${D=lfloorfrac{AB}{C} floor}$，我们用long double搞。那么最后的答案就是${AB-CD}$，我们直接long long搞，可以视作是在模${2^{64}}$的意义下运算。什么鬼嘛。。。

　　可以long long搞的原因应该是这样的。 ${AB}$与${CD}$不同的位数不会超过long long范围，所以更高位都是相等的，我们就直接不管好了。

细节

　　竟然推错矩阵了×_×

代码

// bzoj2875
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#define LL long long
#define inf 2147483640
#define Pi acos(-1.0)
#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;
 
LL a,m,n,g,c,x0;
LL f[3][3],tmp[3][3],t[3][3];
 
LL mul(LL a,LL b) {
    LL ans=a*b-(LL)((long double)a*b/m+1e-6)*m;   //一定要用long double
    return ans<0 ? ans+m : ans;   //可能减成负数
}
void power(LL b) {
    while (b) {
        if (b&1) {
            for (int i=1;i<=2;i++)
                for (int j=1;j<=2;j++) {
                    tmp[i][j]=0;
                    for (int k=1;k<=2;k++) tmp[i][j]=(tmp[i][j]+mul(f[i][k],t[k][j]))%m;
                }
            for (int i=1;i<=2;i++)
                for (int j=1;j<=2;j++) f[i][j]=tmp[i][j];
        }
        b>>=1;
        for (int i=1;i<=2;i++)
            for (int j=1;j<=2;j++) {
                tmp[i][j]=0;
                for (int k=1;k<=2;k++) tmp[i][j]=(tmp[i][j]+mul(t[i][k],t[k][j]))%m;
            }
        for (int i=1;i<=2;i++)
            for (int j=1;j<=2;j++) t[i][j]=tmp[i][j];
    }
}
int main() {
    scanf("%lld%lld%lld%lld%lld%lld",&m,&a,&c,&x0,&n,&g);
    f[1][1]=x0;f[1][2]=1;
    t[1][1]=a;t[2][1]=c;t[2][2]=1;
    power(n);
    printf("%lld",f[1][1]%g);
    return 0;
}