SA(模拟退火算法)求解TSP问题
步骤
读取文件生产坐标矩阵和距离矩阵
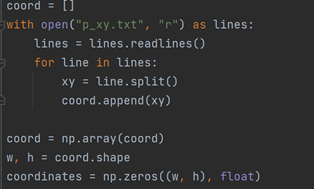
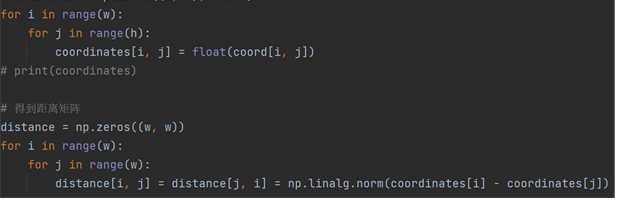
Step1初始化
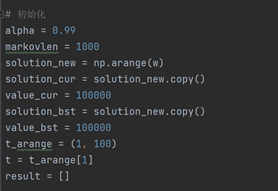
Step2定义当前状态的状态邻域转移
1 随机产生两点a、b(a<b),交换状态序列中a、b位置的值。

2 随机产生三点a、b、c,将当前状态序列中[a:b]的值移到位置c的后面。
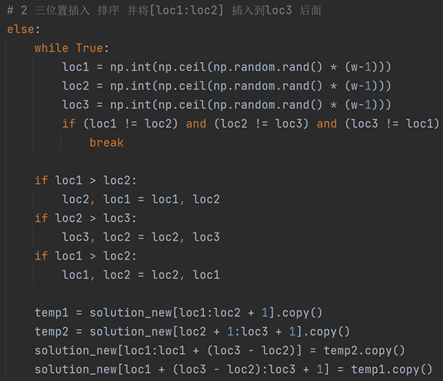
3 随机产生两个点a、b,将当前状态序列[a:b]内的子序列全部反转。
(前两个对于求解15城市的TSP已足够)
Step3计算cost(i),与当前cost比较,并依概率更新当前cost值。
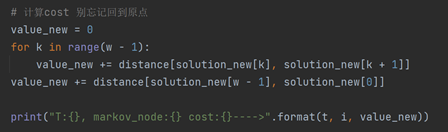

Step4 温度下降、保存当前最优解

求解结果
状态序列运行结果图

状态序列图以及cost损失函数图
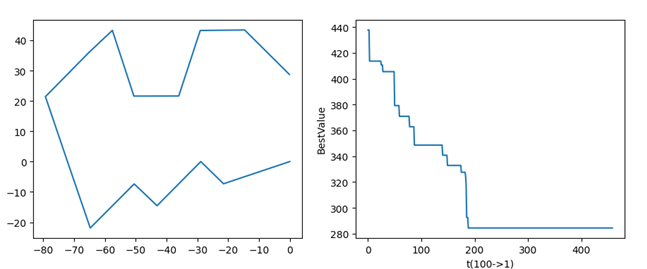
算法思想
利用模拟退火算法的思想求解TSP问题,将TSP不同的解(回路)看作不同的状态,其cost值是各个城市总的距离值之和,求解TSP问题其实就是在N!的空间状态下找到cost值最小的那个状态,但是由于N!极为庞大,若进行遍历搜索会导致NP难问题,所以我们采用模拟退火的算法来求解。首先初始化初始状态、温度t、温度下降系数α、马尔科夫链长度、初始cost等,然后在初始状态的邻域里面寻找n个不同的状态(n为马尔科夫链的长度)并分别计算不同状态的cost(i),若cost>cost(i),表明当前状态距离更短,将解更新为当前状态;如果cost<cost(i),则依概率(P=exp(-(cost(i)-cost)/t))更新解为当前状态;直至(状态数>n)马尔科夫链结束,根据(P=exp(-(cost(i)-cost)/t))更新下降温度值,直至低于阈值,或长时间cost不变;结束,输出解。
代码:
import numpy as np
import matplotlib.pyplot as plt
# 处理数据
coord = []
with open("p_xy.txt", "r") as lines:
lines = lines.readlines()
for line in lines:
xy = line.split()
coord.append(xy)
coord = np.array(coord)
w, h = coord.shape
coordinates = np.zeros((w, h), float)
for i in range(w):
for j in range(h):
coordinates[i, j] = float(coord[i, j])
# print(coordinates)
# 得到距离矩阵
distance = np.zeros((w, w))
for i in range(w):
for j in range(w):
distance[i, j] = distance[j, i] = np.linalg.norm(coordinates[i] - coordinates[j])
# SA
# 初始化
alpha = 0.99
markovlen = 1000
solution_new = np.arange(w)
solution_cur = solution_new.copy()
value_cur = 100000
solution_bst = solution_new.copy()
value_bst = 100000
t_arange = (1, 100)
t = t_arange[1]
result = []
while t > t_arange[0]:
for i in range(markovlen):
# 在邻域内随机产生新解
# 1 位置交换
if np.random.rand() > 0.5:
while True:
loc1 = np.int(np.ceil(np.random.rand() * (w-1)))
loc2 = np.int(np.ceil(np.random.rand() * (w-1)))
if loc1 != loc2:
break
solution_new[loc1], solution_new[loc2] = solution_new[loc2], solution_new[loc1]
# 2 三位置插入 排序 并将[loc1:loc2] 插入到loc3 后面
else:
while True:
loc1 = np.int(np.ceil(np.random.rand() * (w-1)))
loc2 = np.int(np.ceil(np.random.rand() * (w-1)))
loc3 = np.int(np.ceil(np.random.rand() * (w-1)))
if (loc1 != loc2) and (loc2 != loc3) and (loc3 != loc1):
break
if loc1 > loc2:
loc2, loc1 = loc1, loc2
if loc2 > loc3:
loc3, loc2 = loc2, loc3
if loc1 > loc2:
loc1, loc2 = loc2, loc1
temp1 = solution_new[loc1:loc2 + 1].copy()
temp2 = solution_new[loc2 + 1:loc3 + 1].copy()
solution_new[loc1:loc1 + (loc3 - loc2)] = temp2.copy()
solution_new[loc1 + (loc3 - loc2):loc3 + 1] = temp1.copy()
# # 3 区间内反转
# if np.random.rand() > 0.5:
# while True:
# loc1 = np.int(np.ceil(np.random.rand() * w))
# loc2 = np.int(np.ceil(np.random.rand() * w))
# if loc1 != loc2:
# break
# 计算cost 别忘记回到原点
value_new = 0
for k in range(w - 1):
value_new += distance[solution_new[k], solution_new[k + 1]]
value_new += distance[solution_new[w - 1], solution_new[0]]
print("T:{}, markov_node:{} cost:{}---->".format(t, i, value_new))
if value_new < value_cur:
# print("---Accept---")
value_cur = value_new
solution_cur = solution_new.copy()
if value_new < value_bst:
# print("---Best---")
value_bst = value_new
solution_bst = solution_new.copy()
elif np.random.rand() < np.exp(-(value_new - value_cur) / t):
# print("---概率接受---")
value_cur = value_new
solution_cur = solution_new.copy()
else:
# print("---拒绝接受---")
value_new = value_cur
solution_new = solution_cur.copy()
# 温度下降
t = t * alpha
result.append(value_bst)
print("---Best_Plan_Cost_Now:{}---".format(value_bst))
for i in range(w):
print(solution_bst[i] + 1, end="--->")
print(solution_bst[0] + 1)
print("Cost:{}".format(value_bst))
# 画图
cor_cur = np.array((w+1, h))
for i in range(w):
cor_cur[i, :] = coordinates[solution_bst[i], :].copy()
plt.figure(figsize=(20, 20))
plt.subplot(1, 2, 1)
plt.plot(cor_cur[:, 0], cor_cur[:, 1])
plt.subplot(1, 2, 2)
plt.plot(np.array(result))
plt.ylabel("BestValue")
plt.xlabel("t({}->{})".format(t_arange[1], t_arange[0]))
plt.show()