反向传播的推导

推导过程

TIPs

• (z=Wx,frac{partial z}{partial x}=W)
  • 假设(W)是(n*m)的矩阵，(x)是(m*1)的矩阵，则函数(z)做的事情就是把输入(x:m*1)变为(y:n*1)的向量
  • 显然(z_i=sum^m_{k=1}W_{ik}x_k)，推导过程如下：(，当和相等时为(frac{partial z}{partial x})_{ij}=frac{partial z_i}{partial x_j}=frac{partial}{partial x_j}(sum^m_{k=1}W_{ik}x_k)=sum^m_{k=1}W_{ik}frac{partial}{partial x_j}x_k=W_{ij}，(frac{partial}{partial x_j}x_k当k和j相等时为1))，这个值也是Jacobian矩阵中对应位置的值
• (z=xW,frac{partial z}{partial x}=W^T)
  • 和上面那个类似可以推出这个结果
• (z=x,frac{partial z}{partial x}=I)
  • 因为(frac{partial}{partial x_j}x_k)当k和j相等时为1，否则为0，则Jacobian矩阵中对角线的值全为1，是单位矩阵
  • 类似的，我们可以想到如果(z=f(x))，那么对角线上对应的值为(f'(x_i))，即此时(frac{partial z}{partial x}=diag(f'(x)))，且(diag(f'(x))I=circ f'(x))
• (z=Wx,delta = frac{partial J}{partial z},frac{partial J}{partial W}=frac{partial J}{partial z}frac{partial z}{partial W}=deltafrac{partial z}{partial W})中的(delta)
  • (J)是损失函数，输出为标量，那么对(W)的Jacobian矩阵就是(1*nm)大小的矩阵，因为(W)的大小为(nm)，但实际上的处理方法是将矩阵调整为和(W)一样的大小（比较方便），这样处理带来的问题是：(z)是一个向量(n×1)，那么(frac{partial z}{partial W})的大小会是(n×m×n)！，为了避免这个问题引入记号(delta)，则(frac{partial J}{partial W}=delta^Tx^T)，因为(delta)是(1*n)，(x)是(m*1)，则按前面式子计算出来的结果就是(n*m)
  • 稍微修改条件，(z=xW)，那么对应的为(frac{partial J}{partial W}=x^Tdelta)
• (hat y=softmax( heta),J=CrossEntropy(y,hat y)) ,(frac{partial J}{partial heta}=hat y-y)

举例

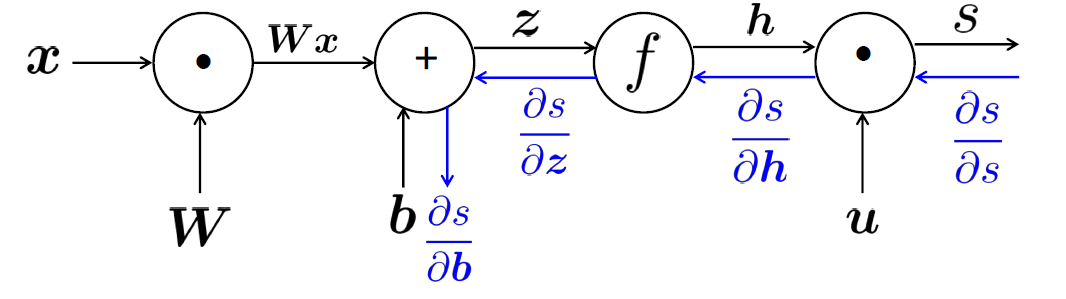
• (z=Wx+b)，(h=f(z))，(s=u^Th)
• (frac{partial s}{partial W}=frac{partial s}{partial h}frac{partial h}{partial z}frac{partial z}{partial W})，(frac{partial s}{partial b}=frac{partial s}{partial h}frac{partial h}{partial z}frac{partial z}{partial b})
  • 令(delta)为(frac{partial s}{partial h}frac{partial h}{partial z})，避免重复计算，且(delta=u^Tcirc f'(z))
  • 单独看(frac{partial s}{partial W_{ij}}=delta_ix_j)，(delta_i)是从终点反向传播回去积累的，(x_j)是(j)节点对应用的函数的梯度
  • 不断运用链式法则将误差反向传播回去，灵活运用(delta)避免重复运算

Reference

1. 斯坦福cs224n深度学习自然语言处理