BN的深度理解:https://www.cnblogs.com/guoyaohua/p/8724433.html
BN:
BN的意义:在激活函数之前将输入归一化到高斯分布,控制到激活函数的敏感区域,避免激活函数的梯度饱和导致梯度消失,增加学习效率
(1)加速收敛(2)控制过拟合,可以少用或不用Dropout和正则(3)降低网络对初始化权重不敏感(4)允许使用较大的学习率
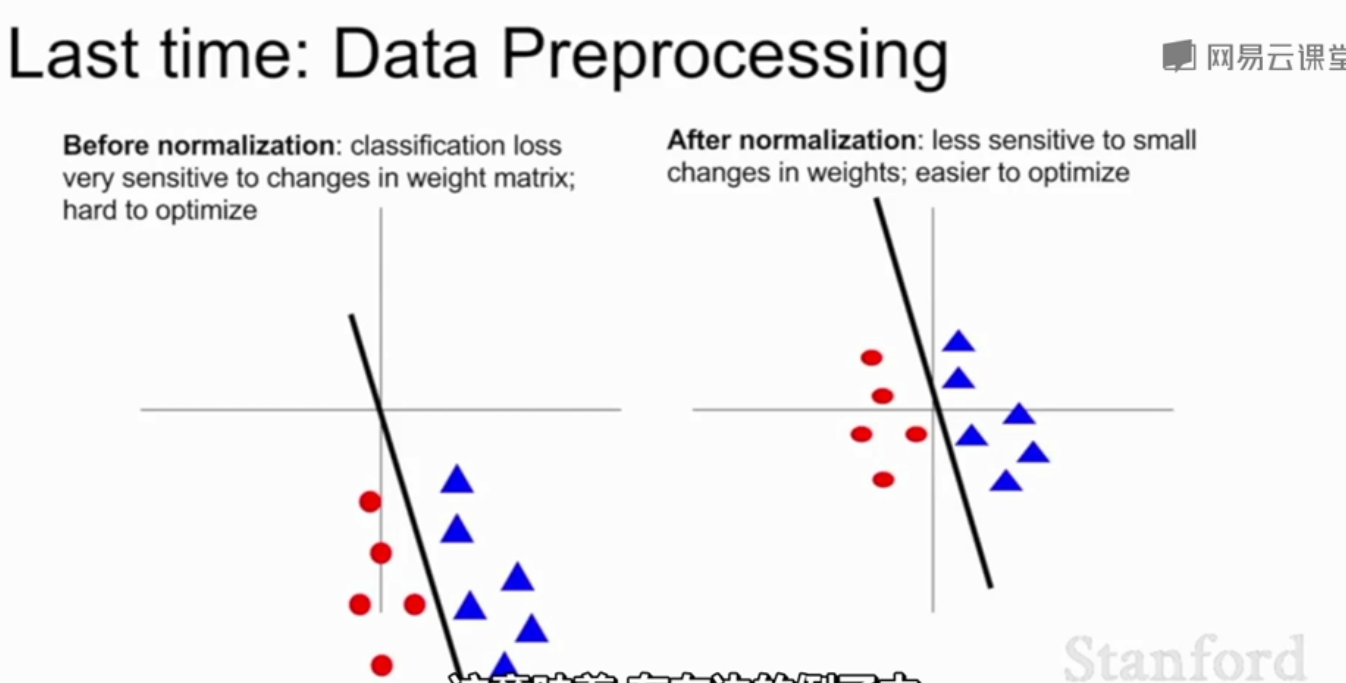
上图中,左边的例子,损失函数对权重微小的变动(分类器旋转偏移)较为敏感,归一化后损失函数对权重微小的变动不那么敏感了 ,让网络学习变得更容易

一般在全连接或卷积层之后非线性层之前采用BN:

在完成批量归一化操作之后,需要进行额外的缩放操作:对常量γ及进行缩放,再用另一个β因子进行平移(相当于回复恒等函数,如果需要的话),如果网络需要可以学习缩放因子γ使之等于方差,学习β使之等于均值,

根据输入先求出mini—batch的均值和方差,减去均值除以方差得到高斯分布(实践中无需完全吻合),最后缩放和偏移


监视训练:
1.数据预处理,零均值化
2.选择网络结构
3.初始化网络,检查loss函数是否合理,检查正则化项
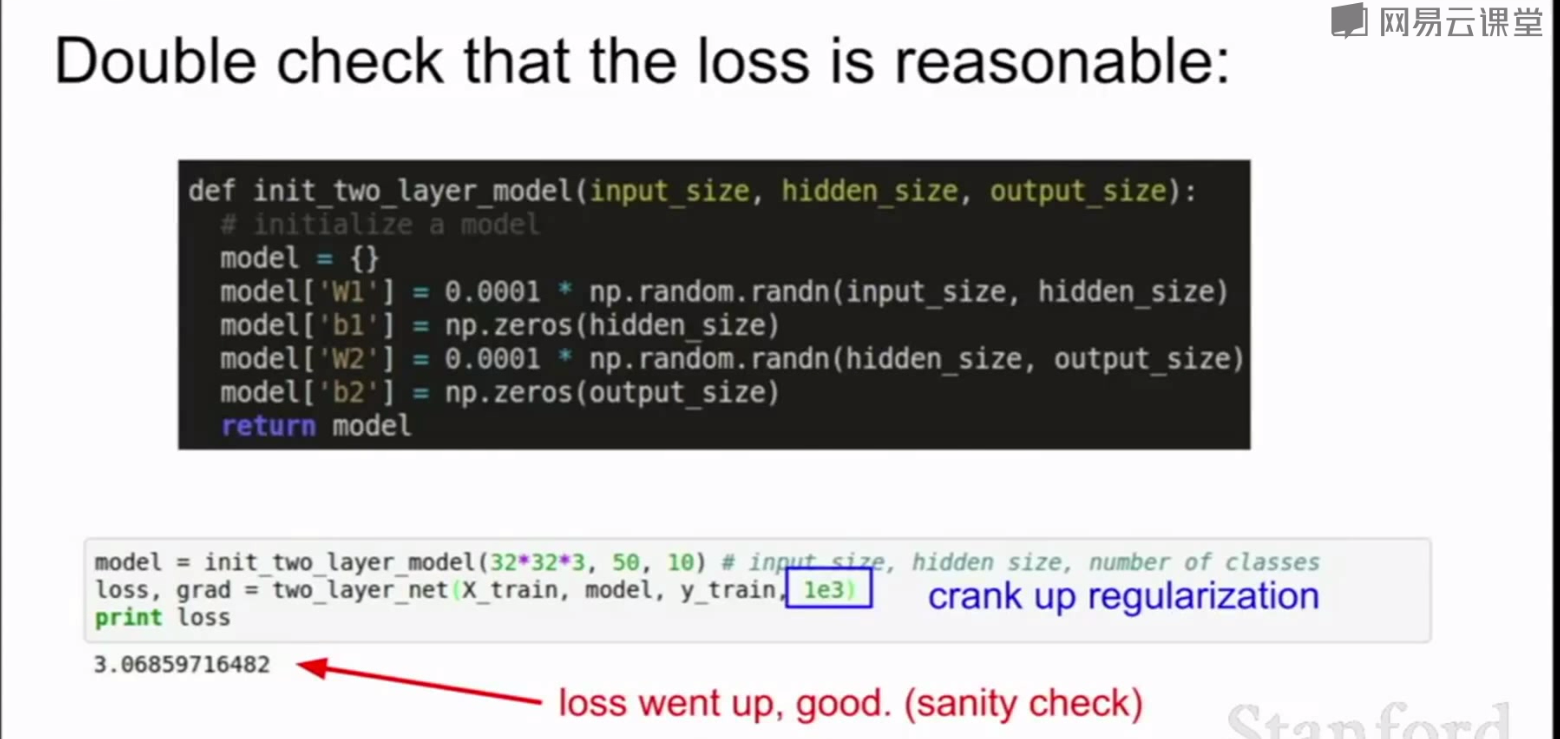
4.设置合理的学习率
超参数优化:
交叉验证
1