Insert or Merge

• 题目描述

• 题目思路

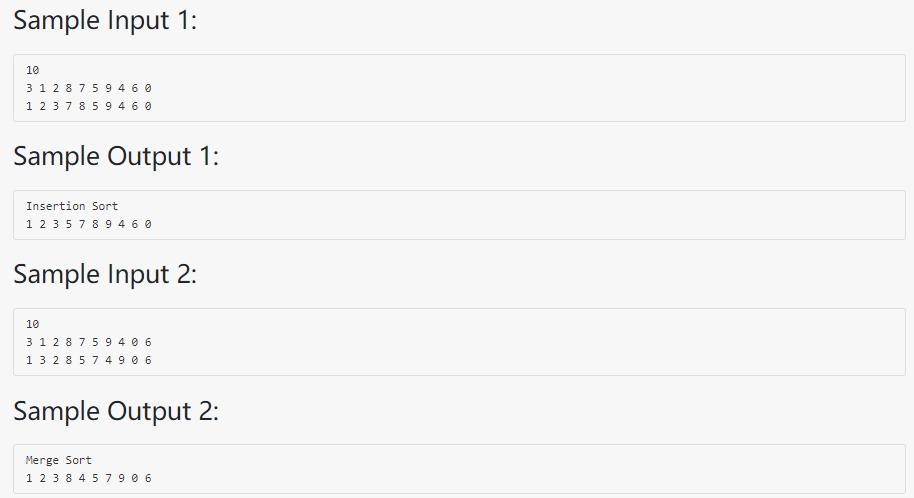
1 第一步是如何区分插入排序和归并排序，插入排序前面一部分是有序的，后面一部分尚未处理的序列没有变化。

2 继续迭代
(1) 插入排序的继续迭代比较好实现，只要从无序部分的第一个元素开始执行一次循环即可。
(2) 归并排序的难点在于找到归并段，在找到正确的归并段后，将非递归的归并排序执行一趟即可。
判断归并段长度的代码如下：

//计算归并段的长度并返回归并段长度
int MergeLength(int *B,int N)
{
	int l = 0;
	int i = 0;
	for (l = 2;l <= N;l = l * 2)
	{
		for (i = l;i < N;i = i + l * 2)
		{
			if (B[i] < B[i-1])
			{
				break;
			}
		}
		if (i < N)
		{
			break;
		}
	}
	return l;
}

• C语言实现

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>

int IsInsertion(int *A,int *B,int N)
{
	int i, k;
	for (i = 1;i < N;i++)
	{
		if (B[i] < B[i-1])
		{
			break;  //发现顺序不对 跳出循环
		}
	}
	k = i;  //保存跳出点 为下一次进行插入排序做准备
	for (;i < N;i++)
	{
		if (A[i] != B[i])
		{
			break;  //后面的序列有变化 说明不是插入排序 而是归并排序
		}
	}
	if (i == N)
	{
		return k;  //是插入排序 返回插入的位置
	}
	else
	{
		return 0;  //不是插入排序
	}
}

void PrintResults(int *B,int N)
{
	for (int i = 0;i < N - 1;i++)
	{
		printf("%d ",B[i]);
	}
	printf("%d", B[N-1]);
}

void NextInsertion(int *B,int N,int K)
{
	int tmp;
	int i = 0;
	printf("Insertion Sort
");
	
	tmp = B[K];

	for (i = K-1;i >= 0;i--)
	{
		if (tmp < B[i])
		{
			B[i + 1] = B[i];
		}
		else
		{
			break;
		}
	}
	B[i + 1] = tmp;
	PrintResults(B,N);
}
//计算归并段的长度并返回归并段长度
int MergeLength(int *B,int N)
{
	int l = 0;
	int i = 0;
	for (l = 2;l <= N;l = l * 2)
	{
		for (i = l;i < N;i = i + l * 2)
		{
			if (B[i] < B[i-1])
			{
				break;
			}
		}
		if (i < N)
		{
			break;
		}
	}
	return l;
}

void NextMerge(int *B,int N)
{
	int p1, p2;
	int i;
	int p;
	int L;  //当前归并段的长度
	int *Tmp;
	printf("Merge Sort
");
	L = MergeLength(B,N);

	Tmp = (int *)malloc(sizeof(int) * N);
	p = 0;  //p指向Tmp中当前处理的位置
	
	for (i = 0;i < (N-L-L);i = i + L + L)  //两两归并长度为L的段
	{
		p1 = i;
		p2 = i + L;  //p1和p2分别指向两个段的当前处理位置
		while ((p1 < (i + L)) && (p2 < (i + L + L)))
		{
			if (B[p1] > B[p2])
			{
				Tmp[p++] = B[p2++];
			}
			else
			{
				Tmp[p++] = B[p1++];
			}
		}  //end while ((p1 < (i + L)) && (p2 < (i + L + L)))
		while (p1 < (i + L))
		{
			Tmp[p++] = B[p1++];
		}
		while (p2 < (i + L + L))
		{
			Tmp[p++] = B[p2++];
		}
	}
	
	if ((N-i) > L)
	{
		p1 = i;
		p2 = i + L;
		while ((p1 < (i+L)) && (p2 < N))
		{
			if (B[p1] > B[p2])
			{
				Tmp[p++] = B[p2++];
			}
			else
			{
				Tmp[p++] = B[p1++];
			}
		}
		while (p1 < (i + L))
		{
			Tmp[p++] = B[p1++];
		}
		while (p2 < (i + L + L))
		{
			Tmp[p++] = B[p2++];
		}
	}
	else
	{
		while (i < N)
		{
			Tmp[i] = B[i++];
		}
	}

	PrintResults(Tmp,N);
}

int main()
{
	int *A;
	int *B;
	int N;
	int k;
	scanf("%d",&N);
	A = (int *)malloc(sizeof(int) * N);
	B = (int *)malloc(sizeof(int) * N);
	
	for (int i = 0;i < N;i++)
	{
		scanf("%d",&A[i]);
	}

	for (int i = 0; i < N; i++)
	{
		scanf("%d", &B[i]);
	}

	if (k = IsInsertion(A,B,N))
	{
		NextInsertion(B,N,k);
	}
	else
	{
		NextMerge(B,N);
	}
	// system("pause");
	return 0;
}