题目描述
有一棵点数为 N 的树,树边有边权。给你一个在 0~ N 之内的正整数 K ,你要在这棵树中选择 K个点,将其染成黑色,并将其他 的N-K个点染成白色 。 将所有点染色后,你会获得黑点两两之间的距离加上白点两两之间的距离的和的受益。问受益最大值是多少。
输入格式
第一行包含两个整数 N, K 。接下来 N-1 行每行三个正整数 fr, to, dis , 表示该树中存在一条长度为 dis 的边 (fr, to) 。输入保证所有点之间是联通的。
输出格式
输出一个正整数,表示收益的最大值。
输入输出样例
3 1 1 2 1 1 3 2
3
说明/提示
对于 100% 的数据, 0<=K<=N <=2000
分析
说实话这道题做的我有点悲伤
先是想了好久没发现自己状态设计错了
后来又调了好久都是80,结果蓦然发现是枚举的上下界有误
好吧还是我自己的锅,因为我的状态设计对上下界的要求太高了
我该庆幸这题没有负权边吗,不然在初值上又要出锅
Part 1 状态
开始的时候,一般都会往
dp[节点][黑点个数] = 距离
这个方向想
然鹅,我卡住了,翻了翻题解,才知道,这么设计状态是不可行的
这么设计状态明显是有后效性的,除非你可以记录方案,实时更新距离
我们再想想,计算多条路径,除了把一条一条的路径加起来,还有没有什么特点,或者其他求法
这时,我们应给可以注意到很多时候,有些边是被重复计算的,尤其是当路径条数多了的时候,这个重复的次数会更多
此时,我们就获得了计算路径和的第二种方法:
计算每条便被计算了多少次,乘以边权,再加起来
看题目的要求: 黑点两两之间的距离加上白点两两之间的距离的和
所以,经过这条边的路径当且仅当两个点分布在这条边的两端且同色
也就是说,这条边的经过的次数,至于两端分布的黑点白点的个数有关,而与方案无关
很容易想到经过这条边的次数就是:
左边黑点个数*右边黑点个数+左边白点个数*右边白点个数
好的,这样的话,状态似乎也水到渠成了
dp[节点编号][黑点个数] = 目前子树的边对于答案的贡献
嗯?有区别吗?
当然有,对答案的贡献,也就是说,我们计算出子树中各条边在答案中的贡献(注意这个贡献是全局的,不仅限于子树内)
Part 2 转移
有了状态,转移会显得明白许多
我们枚举i为子树中的黑点个数,枚举j为儿子子树中的黑点个数,则有方程
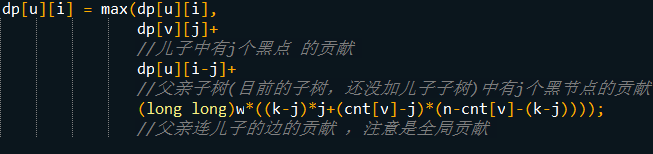
嗯,其实最重要的细节来了
i,j的上下界
首先,i必须倒序,避免重复
i的上界:min(cnt[u],k) 很好想
下界:max(k-(n-cnt[u]),0) 因为i等于k-(n-cnt[u])的时候,正好子树i以外的点(包括没有遍历的儿子)全都是黑色,
如果i小于k-(n-cnt[u]),说明黑点没有到达k个,而出现了这个bug时,在算w的贡献时就会出错
j的上界min(cnt[v],i) 很好想,关键是j的下界:max(k-(n-cnt[v]),max(i-cnt[u]+cnt[v],0))
k-(n-cnt[v])根i一样的原理,不重复阐释了,max(i-cnt[u]+cnt[v],0)主要是源于这个不等式:
cnt[u]-cnt[v]>=i-j,就是父亲子树中剩下的节点要足以容下剩下的黑点
完整的枚举:

代码

1 /***************************** 2 User:Mandy.H.Y 3 Language:c++ 4 Problem:luogu3177 5 Algorithm: 6 *****************************/ 7 8 #include<bits/stdc++.h> 9 10 using namespace std; 11 12 const int maxn = 2e3 + 5; 13 14 int n,k; 15 int size,first[maxn]; 16 int cnt[maxn]; 17 long long dp[maxn][maxn]; 18 19 struct Edge{ 20 int v,w,nt; 21 }edge[maxn << 1]; 22 23 template<class T>inline void read(T &x){ 24 x = 0;char ch = getchar();bool flag = 0; 25 while(!isdigit(ch)) flag |= ch == '-',ch = getchar(); 26 while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar(); 27 if(flag) x = -x; 28 } 29 30 void file(){ 31 freopen("data1.in","r",stdin); 32 // freopen("1311.out","w",stdout); 33 } 34 35 void eadd(int u,int v,int w){ 36 edge[++size].v = v; 37 edge[size].w = w; 38 edge[size].nt = first[u]; 39 first[u] = size; 40 } 41 42 void readdata(){ 43 read(n);read(k); 44 for(int i = 1;i < n; ++ i){ 45 int u,v,w; 46 read(u);read(v);read(w); 47 eadd(u,v,w);eadd(v,u,w); 48 } 49 } 50 51 void dfs(int u,int fa){ 52 cnt[u] = 1; 53 for(int e = first[u];e;e = edge[e].nt){ 54 int v = edge[e].v; 55 if(v == fa) continue; 56 int w = edge[e].w; 57 dfs(v,u);cnt[u] += cnt[v]; 58 for(int i = min(cnt[u],k);i >= max(k-(n-cnt[u]),0); -- i){ 59 for(int j = max(k-(n-cnt[v]),max(i-cnt[u]+cnt[v],0));j <= min(cnt[v],i);++j){ 60 dp[u][i] = max(dp[u][i], 61 dp[v][j]+ 62 //儿子中有j个黑点 的贡献 63 dp[u][i-j]+ 64 //父亲子树(目前的子树,还没加儿子子树)中有j个黑节点的贡献 65 (long long)w*((k-j)*j+(cnt[v]-j)*(n-cnt[v]-(k-j)))); 66 //父亲连儿子的边的贡献 ,注意是全局贡献 67 } 68 } 69 //这个循环写得我很悲伤 70 } 71 } 72 73 void work(){ 74 if(k > n-k) k = n - k; 75 //小优化啦,黑色白色其实是等价的 76 dfs(1,0); 77 printf("%lld",dp[1][k]); 78 } 79 80 int main(){ 81 // file(); 82 readdata(); 83 work(); 84 return 0; 85 }
