MZOJ #82 总统竞选

分析

Part 1 模板题

最优比率生成树，01规划的模板题

但是！

他卡常

所以，孩子们还是乖乖写Dinkelbach吧 

Part 2 01分数规划

欢迎造访我的blog：01分数规划

Part 3 最小值

我们需要求的是

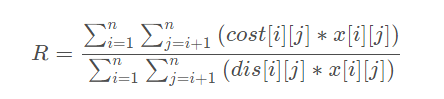
中R的最小值，（x[i][j]代表这条边是否选）

稍微移项变换一下，就变成了：

可以看出，当R 减小的时候，左边的式子的值会增大。

若对于某一个确定的R值，左边的值是可以小于0的，

也就说明存在一个更小的R值能使左边的式子更加接近于0

这样，我们可以增大R 的值再次验证，直到找到最小的R值为止

 当然可以二分解决，验证的时候，以cost[i][j]-R*dis[i][j]为权值求最小生成树

由于是一个完全图，n²的prim显然更优秀，用邻接矩阵存也方便

一切都很好

但是！

恭喜你，TLE快乐

这时，我们就需要更优秀的Dinkelbach算法

简单说来就是直接跳横截距

举个栗子（要糖炒的）

假如我们对于一个R值，找到了一个最小生成树的方案使得生成树上的所有边的权值cost[i][j]-R*dis[i][j]的和小于0

我们下一步就直接跳到令这颗生成树的所有权值和等于0的R上

理论上会快一点

不过这种算法与二分各有千秋，各有擅长的部分，根据题意选择正确适合的就好

看核心代码：

Prim

主程序

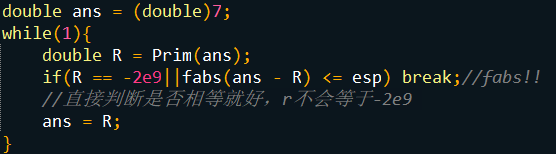
代码

/********************
User：Mandy
Language:c++
Problem:
********************/
#include<bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef double dou;

const int maxn = 1005;
const dou esp = 1e-8;

int t,n,size;
double d[maxn];
int from[maxn];
double dis[maxn][maxn],cost[maxn][maxn];

struct Node{
    int x,y,z;
}node[maxn];


template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
    freopen("build3.in","r",stdin);
    freopen("build.out","w",stdout);
}

void readdata(){
    for(int i = 1;i <= n; ++ i){
        read(node[i].x);
        read(node[i].y);
        read(node[i].z);
    } 
}

double dist(int i,int j){
    return sqrt(((dou)node[i].x - node[j].x) * 
                ((dou)node[i].x - node[j].x) + 
                ((dou)node[i].y - node[j].y) * 
                ((dou)node[i].y - node[j].y));
}

void init(){
    for(int i = 1;i <= n; ++ i){
        for(int j = i;j <= n; ++ j){
            dis[i][j] = dist(i,j);
            dis[j][i] = dis[i][j];
            cost[i][j] = abs((double)node[i].z - node[j].z);
            cost[j][i] = cost[i][j];
        }
    }
}

double Prim(double r){
    int cnt = 1;t = 0;double c = 0,D = 0;
    for(int i = 1;i <= n;++i) 
        d[i] = cost[1][i]-r*dis[1][i],from[i] = 1;
    d[1] = -2e9;
    for(int j = 1;j <= n; ++ j){
        double cur = 2e9;int id = 0;
        for(int i = 1;i <= n; ++ i){
            if(d[i]!=-2e9 && d[i] < cur){
                cur = d[i];    id = i;
            }
        }
        t += cur;cnt++;d[id] = -2e9;
        c += cost[from[id]][id];
        D += dis[from[id]][id];
        if(cnt == n) break;
        for(int i = 1;i <= n; ++ i) {
            if(d[i] > cost[id][i]-r*dis[id][i]){
                d[i] = cost[id][i]-r*dis[id][i];
                from[i] = id;
            }
        }
    }
    if(t < esp) return c/D;
    else return -2e9;
}

void work(){
    double ans = (double)7;
    while(1){
        double R = Prim(ans);
        if(R == -2e9||fabs(ans - R) <= esp) break;//fabs!!
        //直接判断是否相等就好，r不会等于-2e9 
        ans = R;
    }
    printf("%.3lf
",ans);
}

int main(){
//    file();
    while(~scanf("%d",&n)){
        if(!n) break;
        size = 0;
        readdata();
        init();
        work();
    }
    return 0;
}

最后偷偷放个题解