luogu1850 NOIP2016 换教室

题目

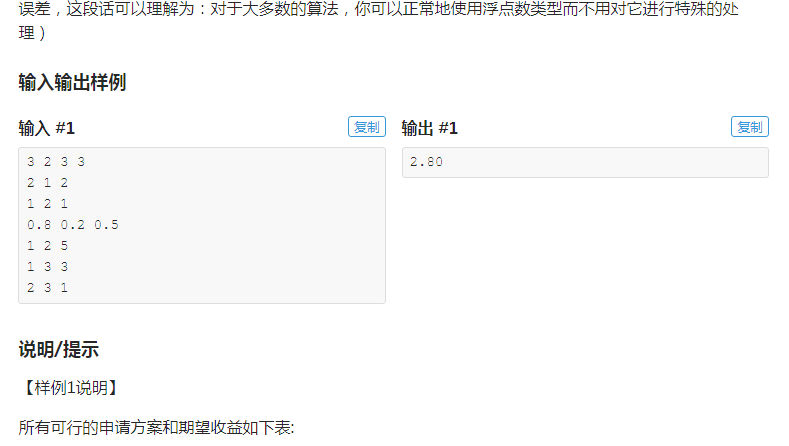
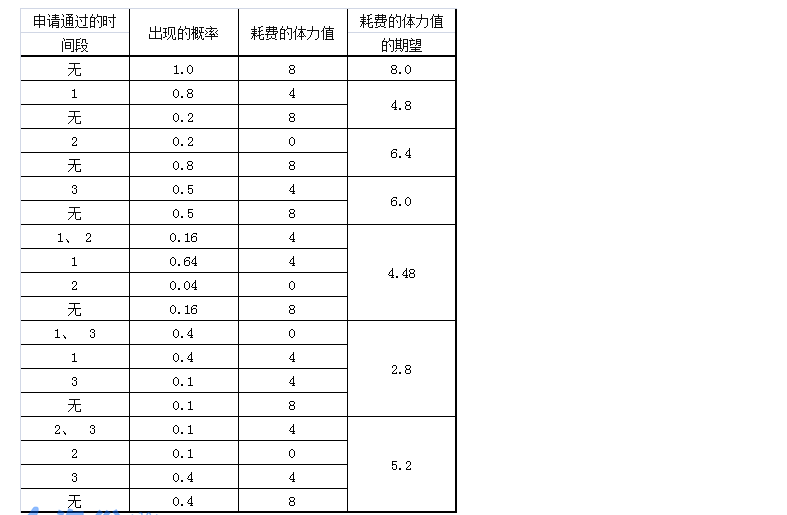
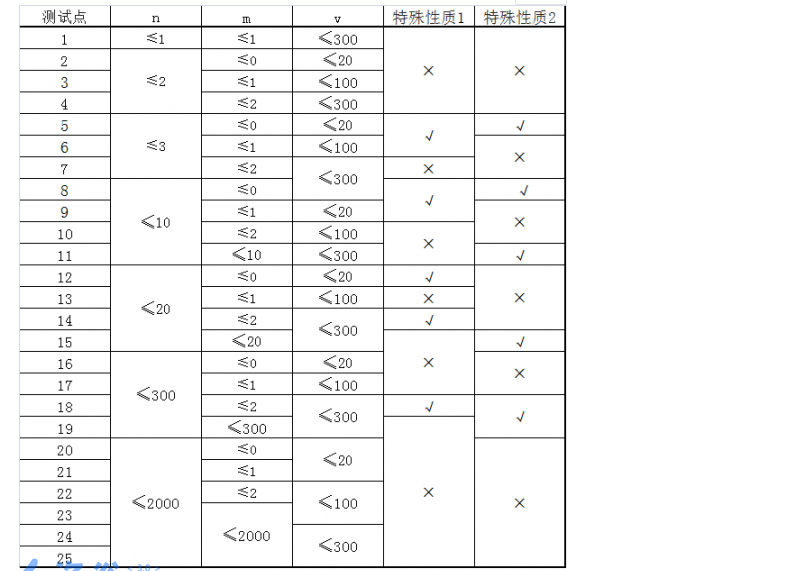
注：以上图片截图自洛谷

分析

 这道题概率DP，前置知识：数学期望

part 1 状态

dp [ 第 i 个时间段 ] [ 换了 j 次 ] [ 当前是否换了 ] = 最优方案的期望值

part 2 转移

我们把期望下放到每条路；

你可以选择申请或不申请；

如果选择申请：期望的路径长 = （申请成功的路径长） * 申请成功概率 + （申请不成功的路径长） * 申请不成功概率

这里注意不要被样例解释误导了，推导一下他们其实是一样的，因为我们的状态是：dp [ 第 i 个时间段 ] [ 换了 j 次 ] [ 当前是否换了 ] = 最优方案的期望值

代码

/*************************
User：Mandy.H.Y
Language:c++
Problem:luogu1850
Algorithm: 
*************************/

#include<bits/stdc++.h>

using namespace std;

const int maxn = 2005;
const int maxv = 305;
const int maxe = 90005;

int n,m,v,e,size;
int c[maxn],d[maxn];
double k[maxn],dp[maxn][maxn][3];
int g[maxv][maxv];

struct Edge{
    int v,nt,w;
}edge[maxe << 1];

template<class T>inline void read(T &x){
    x = 0;bool flag = 0;char ch = getchar();
    while(!isdigit(ch)) flag |= ch == '-',ch = getchar();
    while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar();
    if(flag) x = -x;
}

template<class T>void putch(const T x){
    if(x > 9) putch(x / 10);
    putchar(x % 10 | 48);
}

template<class T>void put(const T x){
    if(x < 0) putchar('-'),putch(-x);
    else putch(x);
}

void file(){
    freopen("1850.in","r",stdin);
    freopen("1850.out","w",stdout);
}

void readdata(){
    memset(g,0x3f3f3f3f,sizeof(g));
    read(n);read(m);read(v);read(e);
    for(int i = 1;i <= v; ++ i) g[i][i] = 0;
    for(int i = 1;i <= n; ++ i) read(c[i]);
    for(int i = 1;i <= n; ++ i) read(d[i]);
    for(int i = 1;i <= n; ++ i) scanf("%lf",&k[i]);
    for(int i = 1;i <= e; ++ i) {
        int u,v,w;
        read(u);read(v);read(w);
        g[u][v] = min(g[u][v],w);
        g[v][u] = g[u][v];
    }
}

void Floyd(){
    for(int l = 1;l <= v; ++ l)
    for(int i = 1;i <= v; ++ i)
    for(int j = 1;j <= v; ++ j){
        if(g[i][l] != 0x3f3f3f3f && g[l][j] != 0x3f3f3f3f)
            if(g[i][l] + g[l][j] < g[i][j]) g[i][j] = g[i][l] + g[l][j];
    }
}

void work(){
    
    Floyd();
    
    for(int i = 2;i <= n; ++ i){
        
        int u1 = c[i - 1],u2 = d[i - 1];
        int v1 = c[i],v2 = d[i];
        
        dp[i][0][0] = dp[i - 1][0][0] + g[u1][v1];
        
        for(int j = 1;j <= m; ++ j){
            
            dp[i][j][0] = min(dp[i - 1][j][0] + g[u1][v1],
                              dp[i - 1][j][1] + 
                              k[i - 1] * g[u2][v1] + 
                              (1 - k[i - 1]) * g[u1][v1]);
            
            dp[i][j][1] = dp[i - 1][j - 1][0] + 
                          k[i] * g[u1][v2] + 
                          (1 - k[i]) * g[u1][v1];
            if(j > 1) dp[i][j][1] = min(dp[i][j][1],dp[i - 1][j - 1][1] + 
                                                    k[i - 1] * k[i] * g[u2][v2] + 
                                                    k[i - 1] * (1 - k[i]) * g[u2][v1] +
                                                    (1 - k[i - 1]) * k[i] * g[u1][v2] +
                                                    (1 - k[i - 1]) * (1 - k[i]) * g[u1][v1]);
        
        }
    }
    double ans = 2000000000.0;
    for(int i = 0;i <= m; ++ i) {
        ans = min(ans,dp[n][i][0]);
        if(i > 0) ans = min(ans,dp[n][i][1]);
    }
    
    printf("%.2lf",ans);
}

int main(){
//    file();
    readdata();
    work();
    return 0;
}