题目
题目描述
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
-
游戏界面是一个长为n ,高为 m 的二维平面,其中有k 个管道(忽略管道的宽度)。
-
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
- 小鸟每个单位时间沿横坐标方向右移的距离为1 ,竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度X ,每个单位时间可以点击多次,效果叠加;
如果不点击屏幕,小鸟就会下降一定高度Y 。小鸟位于横坐标方向不同位置时,上升的高度X 和下降的高度Y 可能互不相同。
- 小鸟高度等于0 或者小鸟碰到管道时,游戏失败。小鸟高度为 m 时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以 ,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
输入输出格式
输入格式:
输入文件名为 bird.in 。
第1 行有3 个整数n ,m ,k ,分别表示游戏界面的长度,高度和水管的数量,每两个
整数之间用一个空格隔开;
接下来的n 行,每行2 个用一个空格隔开的整数X 和Y ,依次表示在横坐标位置0 ~n- 1
上玩家点击屏幕后,小鸟在下一位置上升的高度X ,以及在这个位置上玩家不点击屏幕时,
小鸟在下一位置下降的高度Y 。
接下来k 行,每行3 个整数P ,L ,H ,每两个整数之间用一个空格隔开。每行表示一
个管道,其中P 表示管道的横坐标,L 表示此管道缝隙的下边沿高度为L ,H 表示管道缝隙
上边沿的高度(输入数据保证P 各不相同,但不保证按照大小顺序给出)。
输出格式:
输出文件名为bird.out 。
共两行。
第一行,包含一个整数,如果可以成功完成游戏,则输出1 ,否则输出0 。
第二行,包含一个整数,如果第一行为1 ,则输出成功完成游戏需要最少点击屏幕数,否则,输出小鸟最多可以通过多少个管道缝隙。
输入输出样例
10 10 6 3 9 9 9 1 2 1 3 1 2 1 1 2 1 2 1 1 6 2 2 1 2 7 5 1 5 6 3 5 7 5 8 8 7 9 9 1 3
1 6
10 10 4 1 2 3 1 2 2 1 8 1 8 3 2 2 1 2 1 2 2 1 2 1 0 2 6 7 9 9 1 4 3 8 10
0 3
说明
【输入输出样例说明】
如下图所示,蓝色直线表示小鸟的飞行轨迹,红色直线表示管道。
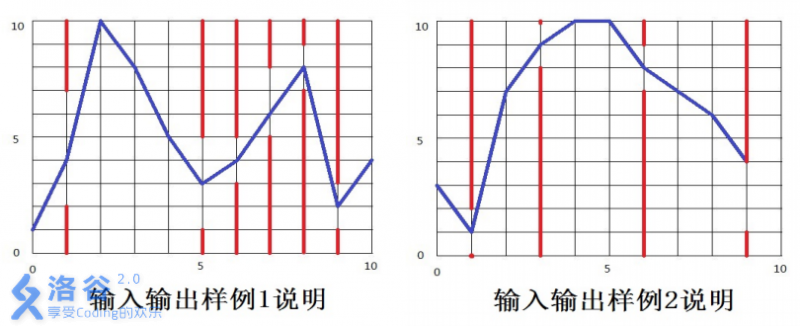
【数据范围】
对于30% 的数据:5 ≤ n ≤ 10,5 ≤ m ≤ 10,k = 0 ,保证存在一组最优解使得同一单位时间最多点击屏幕3 次;
对于50% 的数据:5 ≤ n ≤ 2 0 ,5 ≤ m ≤ 10,保证存在一组最优解使得同一单位时间最多点击屏幕3 次;
对于70% 的数据:5 ≤ n ≤ 1000,5 ≤ m ≤ 1 0 0 ;
对于100%的数据:5 ≤ n ≤ 100 0 0 ,5 ≤ m ≤ 1 0 00,0 ≤ k < n ,0<X < m ,0<Y <m,0<P <n,0 ≤ L < H ≤ m ,L +1< H 。
分析
这道题很容易想到是背包,难点大概就是各种状态的判断
根据题目,可以将小鸟的飞行分为上升和下降两个部分分别判断,也就是分成完全背包和01背包两部分
上升:path [ i ][ j ],表示当前由上升到达j高度所需最少点击数,一个时间可多次点击,所以当成完全背包
下降:drop [ i ][ j ],表示当前由下降到达j高度所需最少点击数,因为一个单位时间只能下降一次,故用当成01背包方法
用了背包的迭代求解,只是注意需要保留上一个单位时间的数据
一个关于顶层的特判,详见代码
代码
1 /* 2 ID:Mandy 3 language:c++ 4 problem:luogu1941 bird 5 */ 6 #include<bits/stdc++.h> 7 8 #define M 1002 9 #define N 10002 10 #define Max(x,y) (x)>(y)?(x):(y) 11 #define Min(x,y) (x)<(y)?(x):(y) 12 #define up(i,l,r) for(int i=l;i<=r;++i) 13 #define down(i,l,r) for(int i=r;i>=l;--i) 14 15 using namespace std; 16 17 int n,m,k,path[3][M],drop[3][M];//滚动数组存背包 18 //path记录小鸟当前上升的路线最少次数,drop是当前下降的最少点击次数 19 struct Conduit 20 { 21 int pos,ovr,bot; 22 }cdt[M];//管道 pos-位置,ovr-管道缝隙的上边沿高度,bot-管道缝隙的下边沿高度 23 struct Rule 24 { 25 int inc,dec; 26 }rule[N];//飞翔规则 inc-上升高度,dec-下降高度 27 28 inline int read() 29 { 30 int x=0; char c=getchar(); 31 while(c<'0'||c>'9') c=getchar(); 32 while(c>='0'&&c<='9') {x=(x<<3)+(x<<1)+(c^48);c=getchar();} 33 return x; 34 } 35 36 inline void put(int x) 37 { 38 if(x==0) {putchar('0'); return;} 39 int num=0; char c[15]; 40 while(x){c[++num]=(x%10)^48; x/=10;} 41 while(num) putchar(c[num--]); 42 } 43 //输入输出优化 44 void docu() 45 { 46 freopen("bird.in","r",stdin); 47 // freopen("bird.out","w",stdout); 48 } 49 50 bool cmp(Conduit a,Conduit b) 51 { 52 return a.pos<b.pos; 53 } 54 55 void readdata() 56 { 57 n=read(); 58 m=read(); 59 k=read(); 60 up(i,1,n) 61 { 62 rule[i].inc=read(); 63 rule[i].dec=read(); 64 } 65 up(i,1,k) 66 { 67 cdt[i].pos=read(); 68 cdt[i].bot=read(); 69 cdt[i].ovr=read(); 70 } 71 sort(cdt+1,cdt+k+1,cmp); 72 //注意输入数据并没有按管道从前往后的顺序 ,所以需要排序 73 } 74 75 void work() 76 { 77 int minans=1<<30; 78 int num=1,now,pre;//num是指当前还未经过的管道的编号 79 int preu=1; 80 int prev=m;//preu-上次能飞到的最低位置,prev-上次能飞到的最高位置 81 int u=1,v=m;//u-能飞到的最低位置,v- 能飞到的最高位置 82 up(i,1,n) 83 { 84 now=i&1;//now指当前在背包中的位置 85 pre=1-now;//指上一个单位时间在背包中的位置 86 bool judge=0; 87 preu=u; 88 prev=v; 89 u=1,v=m; 90 if(cdt[num].pos==i)//如果当前位置有管道 91 { 92 u=cdt[num].bot+1; 93 v=cdt[num].ovr-1;//管道占了的位置不能飞了 ,u是下限,v是上限 94 num++; 95 } 96 if(v==m)//如果可以到达顶层 97 { 98 if(m==prev) path[now][m]=path[pre][m]+1;//如果上一个单位时间也可以到达顶层 99 else path[now][m]=0x3f3f3f3f; 100 } 101 102 up(j,1,m) 103 { 104 if(j!=m) path[now][j]=0x3f3f3f3f; 105 drop[now][j]=0x3f3f3f3f;//初始化 106 107 //上升 因为完全背包要覆盖叠加,所以从1到m都要算 108 int ht=j-rule[i].inc;//ht是指能到达j高度的上一单位时间的高度 109 if(j>v||j<u)//如果这次不能到达j高度 这里的值用于叠加 110 { 111 if(ht>=preu) 112 { 113 if(ht<=prev) path[now][j]=Min(path[now][ht]+1,Min(path[pre][ht]+1,drop[pre][ht]+1)); 114 else path[now][j]=Min(path[now][ht]+1,path[now][j]); 115 } 116 } 117 else 118 { 119 if(ht>=preu&&ht<=prev) path[now][j]=Min(Min(path[now][j],drop[pre][ht]+1),path[pre][ht]+1); 120 if(ht>=1) path[now][j]=Min(path[now][j],path[now][ht]+1);//注意一维与二维的条件要相符 121 } 122 123 ht=j+rule[i].dec;//下落 下落不能叠加或上升,故特判 124 if(ht<=prev&&ht>=preu&&j<=v&&j>=u) drop[now][j]=Min(path[pre][ht],drop[pre][ht]); 125 126 if(v==m)//顶层特判 127 { 128 129 int q=(m-j)/rule[i].inc; 130 if(q*rule[i].inc!=m-j||j==m) q++; 131 132 if(j<=prev&&j>=preu) path[now][m]=Min(path[now][m],Min(drop[pre][j]+q,path[pre][j]+q)); 133 path[now][m]=Min(path[now][m],path[now][j]+q); 134 } 135 136 if(path[now][j]<0x3f3f3f3f||drop[now][j]<0x3f3f3f3f) judge=1;//如果可以通过 137 } 138 if(judge==0)//如果不能通过 139 { 140 putchar('0'); 141 putchar(' '); 142 put(num-2);//num记录当前未到达的管道的编号,如果当前到达的管道不能通过,通过的管道应有num-2个 143 return; 144 } 145 } 146 putchar('1'); 147 putchar(' '); 148 up(i,u,v) minans=Min(minans,Min(path[now][i],drop[now][i]));//注意drop不要忘了 149 put(minans); 150 }
int main()
{
// docu();
readdata();//读入数据
work();
return 0;
}