题目链接 https://codeforces.com/problemset/problem/1228/B
Suppose there is a h×wh×w grid consisting of empty or full cells. Let's make some definitions:
- riri is the number of consecutive full cells connected to the left side in the ii-th row (1≤i≤h1≤i≤h). In particular, ri=0ri=0 if the leftmost cell of the ii-th row is empty.
- cjcj is the number of consecutive full cells connected to the top end in the jj-th column (1≤j≤w1≤j≤w). In particular, cj=0cj=0 if the topmost cell of the jj-th column is empty.
In other words, the ii-th row starts exactly with riri full cells. Similarly, the jj-th column starts exactly with cjcj full cells.
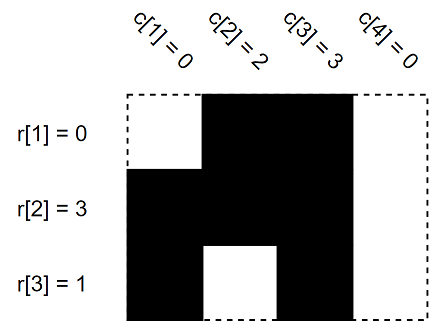
These are the rr and cc values of some 3×43×4 grid. Black cells are full and white cells are empty.You have values of rr and cc. Initially, all cells are empty. Find the number of ways to fill grid cells to satisfy values of rr and cc. Since the answer can be very large, find the answer modulo 1000000007(109+7)1000000007(109+7). In other words, find the remainder after division of the answer by 1000000007(109+7)1000000007(109+7).
The first line contains two integers hh and ww (1≤h,w≤1031≤h,w≤103) — the height and width of the grid.
The second line contains hh integers r1,r2,…,rhr1,r2,…,rh (0≤ri≤w0≤ri≤w) — the values of rr.
The third line contains ww integers c1,c2,…,cwc1,c2,…,cw (0≤cj≤h0≤cj≤h) — the values of cc.
Print the answer modulo 1000000007(109+7)1000000007(109+7).
3 4
0 3 1
0 2 3 0
2
1 1
0
1
0
19 16
16 16 16 16 15 15 0 5 0 4 9 9 1 4 4 0 8 16 12
6 12 19 15 8 6 19 19 14 6 9 16 10 11 15 4
797922655
In the first example, this is the other possible case.
In the second example, it's impossible to make a grid to satisfy such rr, cc values.
In the third example, make sure to print answer modulo (109+7)(109+7).
大致题意就是给一个h × w的矩形，每一单位长宽有一个参数，参数表示这一单位的h（w）所对应的小矩形前r【i】（c【i】）有多少个边长为1的小正方形是涂黑的，问有多少种涂法。
刚看完题有点懵，不知道什么意思（英语渣），画了个图结合一下样例和提示大概明白了，当时的理解就是前r【i】+1和前c【i】+1是固定的，所以把每个点位遍历一遍，如果横纵坐标i，j都是大于r【i】， c【i】的，那么就*2。
三十行代码敲完，测样例，高潮来了，我测了第一组样例过了，然后往下翻，我也不知道哪根神经出了问题，直接测到第三组样例去了，第三组样例也过了，然后就直接提交，wrong answer on test 2。 我当时 ？？？？？？？？？因为我当时测了两组数据都过了，我就以为前两个样例肯定是能过的，结果样例2wa了，赶紧回去看了一下样例，才发现漏了一组数据。再测这组， 1， 1， 0， 1.输出0，可能是最近有点膨胀的原因，也没仔细看样例，下意识直接认为是没有点可以摇摆的时候输出0，就在输出的时候加了一个判断if（ans==1）输出0，wrong answer on test 4，我？？？？？先入为主的我还没有意识到问题的严重性，想了二十分钟以后毫无进展的我骂了一句垃圾题目之后去写C题了……………………………………很脑残对吧，我现在想想也觉得很脑残，这是人能做出来的事吗？没有点可以摇摆的时候最差不也是输出1吗？最近这段时间写的题目基本会加一句保证数据合理或者答案存在，导致这道题即使没加这一句我也下意识当做是这样的数据了，然而其实样例就已经说明了一切，我还是李青附体的跳过了出题人对我的关爱，众所周知，电子竞技不需要视力，唉唉唉唉唉唉唉，掉了102分啊！！！
赛后看了一下学长们的代码，感觉都有点繁琐，看了两眼就没看了，在和学长下棋的时候知道了原来还有不存在的情况，当场心态没了，第七滚粗之后准备第二天再来补题。
到工作室之后考虑了一下不存在的情况，加了两行代码，就过了…过了…了…，有点难受，来日方长吧。
详见注释。
1 #include<bits/stdc++.h>
2 #define LL long long
3 using namespace std;
4 LL r[1005], c[1005];
5 int main()
6 {
7 LL h, w;
8 LL ans = 1, flag = 0;
9 scanf("%lld%lld", &h, &w);
10 for(int i = 1;i <= h;i++)
11 scanf("%lld", &r[i]);
12 for(int i = 1;i <= w;i++)
13 scanf("%lld", &c[i]);
14 for(int i = 1;i <= h;i++)
15 {
16 for(int j = 1;j <= w;j++)
17 {
18 if((i > (c[j] + 1)) && (j > (r[i] + 1))) //可以摇摆的点
19 ans = ans*2%1000000007;
20 else if((i <= (c[j])) && (j == (r[i] + 1))) //纵看为黑，横看为白时输出0
21 flag = 1;
22 else if((i == (c[j] + 1)) && (j <= (r[i]))) //纵看为白，横看为黑时输出0
23 flag = 1;
24 }
25 }
26 if(flag)
27 printf("0
");
28 else
29 printf("%lld
", ans);
30 return 0;
31 }