数据不平衡的数据处理
1. 前言
什么是不平衡数据呢?顾名思义即我们的数据集样本类别比例不均衡。数据不平衡问题主要存在于有监督机器学习任务中。当遇到不平衡数据时,以总体分类准确率为学习目标的传统分类算法会过多地关注多数类,从而使得少数类样本的分类性能下降。绝大多数常见的机器学习算法对于不平衡数据集都不能很好地工作。
1.1 数据不平衡例子
不平衡数据的场景出现在互联网应用的方方面面,如搜索引擎的点击预测(点击的网页往往占据很小的比例)、电子商务领域的商品推荐(推荐的商品被购买的比例很低)、信用卡欺诈检测、网络攻击识别、癌症检测等等。
主要有以下几种处理数据不平衡的方法
2. 数据层面
2.1 重采样
2.1.1 欠采样(下采样)
欠采样是通过减少丰富类的大小来平衡数据集,当数据量足够时就该使用此方法。通过保存所有稀有类样本,并在丰富类别中随机选择与稀有类别样本相等数量的样本,然后根据平衡的新数据集以进一步建模。
2.1.2 过采样(上采样)
当数据量不足时主要使用过采样,它尝试通过增加稀有样本的数量来平衡数据集,而不是去除丰富类别的样本的数量。通过使用重复、自举或合成少数类过采样等方法(SMOTE)来生成新的稀有样品。
2.2 增加权值
首先根据代价敏感学习,学习一个合理的类别样本分布比例(相当于不同类别的权值)。然后将大类样本随机划分成一系列不相交子集。这些子集的大小由稀有类样本集的数量和预先学习的样本分布比例决定。接下来分别将这些不相交子集跟稀有类样本结合,组成一系列平衡的分类子问题,单独训练成子分类器。最后将这些子分类器的输出进一步学习成组合分类器。这种方法在信用卡非法使用检测问题上大大降低了总代价。
3. 算法层面
集成方法
平衡随机森林的方法,该方法对正类和反类分别进行重采样,重采样多次后采用多数投票的方法进行集成学习。
将boosting算法与SMOTE算法结合成SMOTEBoost算法,该算法每次迭代使用SMOTE生成新的样本,取代原有AdaBoost算法中对样本权值的调整,使得Boosting算法专注于正类中的难分样本。
代价敏感方法
在大部分不平衡分类问题中,稀有类是分类的重点。在这种情况下,正确识别出稀有类的样本比识别大类的样本更有价值。反过来说,错分稀有类的样本需要付出更大的代价。代价敏感学习赋予各个类别不同的错分代价(Cost),它能很好地解决不平衡分类问题。以二分类问题为例,假设正类是稀有类,并具有更高的错分代价,则分类器在训练时,会对错分正类样本做更大的惩罚迫使最终分类器对正类样本有更高的识别率。如Metacost和Adacost等算法。
其他方法
一分类(One Class Learning或异常检测(Novelty Detection)
对于正负样本极不平衡的场景,我们可以换一个完全不同的角度来看待问题:把它看做一分类(One Class Learning)或异常检测(Novelty Detection)问题。这类方法的重点不在于捕捉类间的差别,而是为其中一类进行建模,经典的工作包括One-class SVM等。调整SVM以惩罚稀有类别的错误分类。
4.处理的经验
在正负样本都非常之少的情况下,应该采用数据合成的方式;
在负样本足够多,正样本非常之少且比例及其悬殊的情况下,应该考虑一分类方法(癌症检测);
在正负样本都足够多且比例不是特别悬殊的情况下,应该考虑采样或者加权的方法。
数据不平衡的分类器评价指标
- 分类器评价指标
1.1 混淆矩阵
在数据不平衡的分类任务中,我们不在使用准确率当作模型性能度量的指标,而是使用混淆矩阵、精准率、召回率、F1值当作模型的性能度量指标。
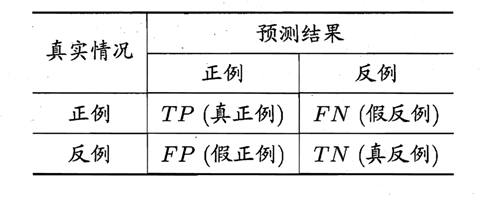
- TP(True Positive):真实是正例,预测也为正例的情况(预测对的部分)
- FP(False Positive):真实是反例,预测为正例的情况(预测错的部分)
- FN(False Negative):真实是正例,预测为反例的情况(预测错的部分)
- TN(True Negative):真实是反例,预测也为反例的情况(预测对的部分)
精准率P
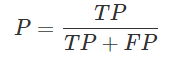
召回率R
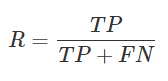
F1值
F1值是精准率和召回率的调和平均值。两个数值的调和平均更加接近两个数当中较小的那个,因此如果要使得F1很高的话那么精准率和召回率都必须很高。
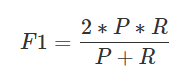
F值的一般情况

PR曲线
精准率和召回率是一个对矛盾的变量。一般精准率(查准率)高,召回率(查全率)就会降低,精准率降低,召回率就会偏高。所以我们可以通过PR曲线来寻找精准率和召回率的平衡点。我们一般可以通过改变分类的阈值来对一个模型的一组结果进行绘制PR曲线。比如针对逻辑回归的一组概率,通过设置阈值分别小于[0,0.1,0.2,...,0.8,0.9,1],来分别计算精准率和召回率,然后绘制出曲线。
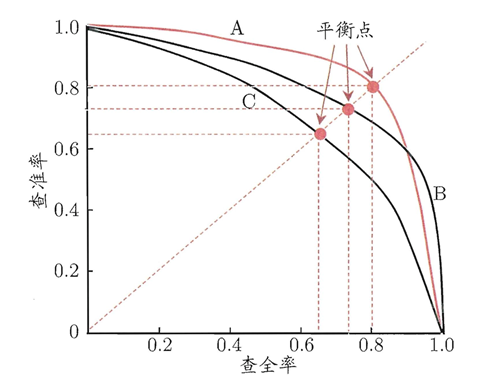
如上图所示,曲线B完全包住了曲线C,我们说曲线B的模型比曲线C的模型要好。
如上图所示的平衡点,基本就是自身曲线的精准率和召回率的平衡的地方,由于这个平衡点比较难评估,所以这时候用F1来近似平衡点。
1.2 ROC和AUC
ROC曲线和PR曲线的原理非常相似,绘制的方式也是通过改变分类的阈值。不同的地方是,ROC是以FPR为X轴和TPR为Y轴进行绘制。PR是以R为X轴,P为Y轴进行绘制。
FPR(False Positive Rate)
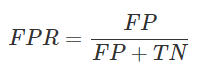
TPR(True Positive Rate)
可以从下公式看出,TPR和召回率是一样的。
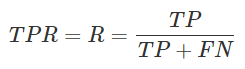

ROC曲线评价标准是,越靠近左上角,模型效果越好。我们用ROC包住的面积叫做AUC,用AUC的大小来衡量模型的优劣。
1.3 代价敏感学习
代价敏感的学习方法是机器学习领域中的一种新方法,它主要考虑在分类中,当不同的分类错误会导致不同的惩罚力度时如何训练分类器。例如在医疗中,"将病人误诊为健康人的代价"与"将健康人误诊为病人的代价"不同;在金融信用卡盗用检测中,"将盗用误认为正常使用的代价"与将"正常使用误认为盗用的代价"也不同。
通常,不同的代价被表示成为一个N×N的Cost矩阵中,其中N是类别的个数。costijcostij表示将一个i类的对象错分到j类中的代价。代价敏感分类就是为不同类型的错误分配不同的代价,使得在分类时,高代价错误产生的数量和错误分类的代价总和最小。
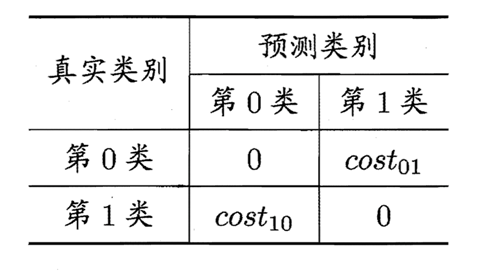
加入了代价矩阵后,错误率的公式改为如下:

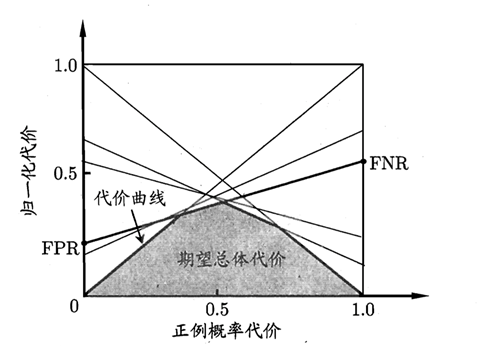
1.4 绘制正例代价曲线
代价曲线的X轴是取值[0,1]的正例概率代价,计算方式如下,其中p是正例的概率:
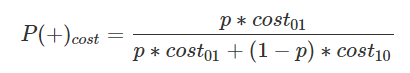
代价曲线的Y轴是取值为[0,1]的归一化代价,FNR是假反例率,FPR是假正例,公式如下:
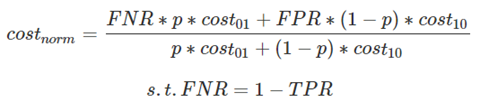
ROC曲线上的每一点对应了代价平面上的一条线段,设ROC曲线上的点的坐标为(TPR,FPR),则可以计算出FNR,然后在代价平面上绘制一条从(0,FPR)到(1,FNR)的直线,直线下的面积代表该条件下的期望总体代价;将ROC上的点全都转换为直线,然后取所有线段下界,围城的面积即为在所有条件下的学习器的期望总体代