一、 实践题目名称----找第k小数
二、 问题描述----在n个无序的整数中找出第k小的数,要求平均时间复杂度为O(n)
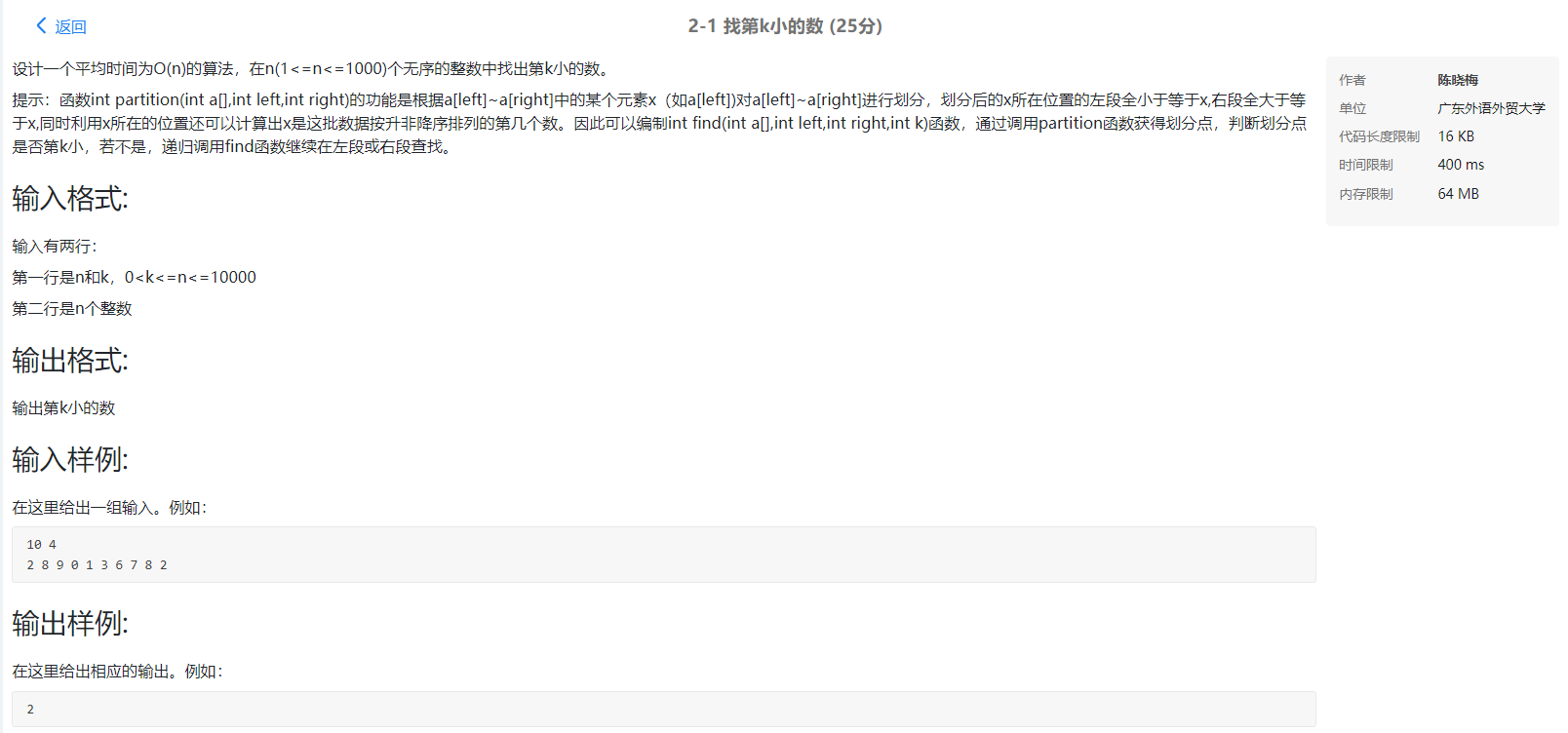
具体题目如图:
三、 算法描述
void FindK (int *a,int left,int right,int k)
{//找第k小
int mid=定位基准位置(调用paritition)
if(mid==第k小,即下标为k-1)
{
cout<<a[mid];//直接输出
}
else if(mid>k-1)
{//第k小的数比mid小,则在mid左段查找
find(a,left,mid-1,k);
}
else
{//第k小的数比mid大,则在mid右段查找
find(a,mid+1,right,k);
}
}
int paritition(int *a,int left,int right)
{//定位基准下标——使得基准左边的数全小于基准,右边的数全大于基准
int i = left,j = right+1;
int x = a[left];
while(1)
{
while(a[++i] < x&&i < right);//从左向右找到大于基准的数
while(a[--j] > x);//从右向左找小于基准的数
if(i >= j)
{//如果i>j,说明所有的数已遍历完,为则退出
break;//此时i下标为大于基准的数,j下标为小于基准的数
}
swap(a[i],a[j]);//交换找到的两个数的位置使得基准左边的数
}
//将基准放在其固定位置
a[left] = a[j];
a[j] = x;
return j;//返回下标位置
}
以下为具体代码实现

#include<iostream>
using namespace std;
int paritition(int *a,int left,int right)
{//定位基准下标
int i = left,j = right+1;
int x = a[left];
while(1)
{
while(a[++i] < x&&i < right);//左侧
while(a[--j] > x);//右侧
if(i >= j)
{
break;
}
swap(a[i],a[j]);
}
a[left] = a[j];
a[j] = x;
return j;
}
void find(int *a,int left,int right,int k)
{//找第k小
int mid=paritition(a,left,right);
if(mid==k-1)
{
cout<<a[mid];//直接输出
}
else if(mid>k-1)
{
find(a,left,mid-1,k);//找左边
}
else{
find(a,mid+1,right,k);//找右边
}
}
int main()
{
int n,k;
cin>>n>>k;
int a[10000];
for(int i=0;i<n;i++)
{
cin>>a[i];
}
find(a,0,n-1,k);
return 0;
}
四、 算法时间及空间复杂度分析
1. 时间复杂度:paritition函数需要遍历整个序列,时间复杂度为O(n), 而FindK函数利用二分思想,且只需要处理一半(最坏情况处理规模为n-1),时间为T(n/2),所以总的T(n) = O(n) + T(n/2) = O(n) + O(nlog21) = O(n) + O(1) = O(n)
2. 空间复杂度:递归算法的空间复杂度 S(n) = 递归深度*每次递归所需辅助空间k
在本题中,递归需要开辟辅助空间,递归深度为log2n, 每次递归所需辅助空间为1,所以递归过程空间复杂度为O(log n),所以总的S(n) = O(1) + O(log n) = O(log n);
五、心得体会
1. 快排能够在每一次确定基准在最终排序序列的确定位置下标,因此找第k小的数能够利用确定基准的位置来比较判断第k小的数应该在哪个范围,从而提高查找的效率。
2. 在此次实践中,需要注意的是:
(1)定位基准的函数里面,利用循环查找大于或小于基准的数时要注意while循环进入的条件,比如从左向右找大于基准的数,循环里应该是小于,则大于时才退出循环得到我们要的数,符号不能乱。
(2)边界问题