第五章小结
一、知识框架(如图)
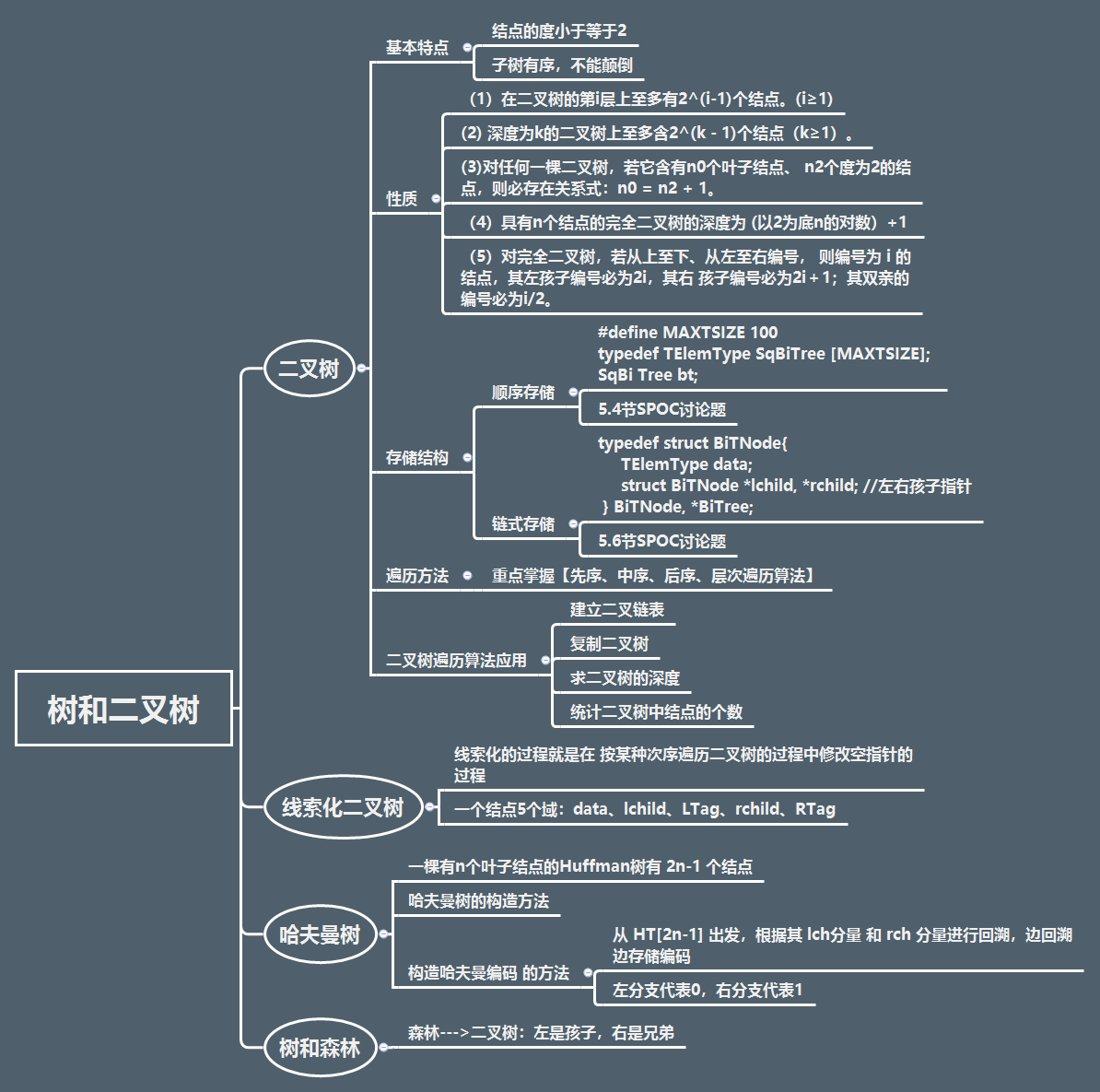
二、二叉树重点掌握算法
1. 先序遍历的递归算法

void PreOrderTraverse(BiTree T) { // 先序遍历二叉树 if(T) { cout << T -> data; //访问根结点 PreOrderTraverse(T->lchild); // 遍历左子树 PreOrderTraverse(T->rchild); //遍历右子树 } }
2.中序遍历、后序遍历与先序遍历相似(顺序不同)
先序:根左右; 中序:左根右 ;后序:左右根
3. 先序建立二叉链表

void CreateBiTree(BiTree &T) {//根据读入的先序字符序列,建立二叉树 cin>>ch; if(ch=='#') T = NULL; //递归结束,建空树 else { T = new BiTNode; T->data = ch; //生成树(子树)的根结点 CreateBiTree(T->lchild); //递归创建左子树 CreateBiTree(T->rchild); //递归创建右子树 } }
4. 先序复制二叉树

void Copy(BiTree T, BiTree &NewT) {//先序复制二叉树 if (T==NULL) { NewT = NULL; return; } //递归结束,建空树 else { NewT = new BiTNode; NewT->data = T->data ; //复制根结点 Copy(T->lchild, NewT->Lchild); //复制左子树 Copy(T->rchild, NewT->rchild); //复制右子树 } }
5. 计算二叉树深度

int Depth(BiTree T) { // 返回二叉树的深度 if(T==NULL) return 0; //空树,故深度为0 else { DepthLeft = Depth(T->lchild); //递归计算左子树的深度 DepthRight = Depth(T->rchild);// 递归计算右子树的深度 return (1+max(DepthLeft,DepthRight)); //左右子树中深度大的+1则为二叉树的深度 } }
6.计算二叉树结点总数

int NodeCount(BiTree T) { //结点个数为左子树的结点个数+右子树的 结点个数再+1。 if(T==NULL) return 0; else return NodeCount(T->lchild) +NodeCount(T->rchild)+1; }
7.按层次顺序遍历二叉树,输出每个结点的 data 值。【层次遍历过程中采用的辅助数据结构是队列,利用其先进先出的特点来进行层次遍历】

typedef struct biTNode { TElemType data; struct biTNode *lchild; struct biTNode *rchild; }BiTNode, *BiTree; //链式二叉树结构体类型 void fun(BiTree T) { //层次遍历输出二叉树 queue<BiTNode *> q;//指向BiTNode类型的指针队列 q.push(T);//T指针入队 BiTNode *p; //辅助变量 while (!q.empty()) { //q非空则继续访问队列 p = q.front(); //取队头 q.pop(); //出队 if (p!=NULL) { cout << p->data;//输出结点data q.push(p->lchild);//左孩子入队 q.push(p->rchild); //右孩子入队 } } }
【给定一棵树,求其最深的叶子结点的编号。测试数据保证只有唯一答案,则利用层次遍历,遍历的最后一个结点即为最深叶子结点】
三、哈夫曼树
1.结点类型定义:
typedef struct { int weight; //权值 int parent, lch, rch; } *HuffmanTree;
2.例子

四、二叉搜索树
1.二叉搜索树(递归&非递归)
https://blog.csdn.net/LYJwonderful/article/details/80315438
2. 二叉搜索树的定义、查找、插入和删除
https://blog.csdn.net/yanxiaolx/article/details/51986428
五、易错点
1. typedef TElemType SqBiTree[MAXTSIZE];
// 定义了一个新类型,名字为 SqBiTree,其本质是一个数组,数组元素类型是 TElemType,长度为 MAXTSIZE
如:int a[100]; int b[100] <---> typedef int Num[100] ; Num a,b;
2.int n; cin >>n ; int *a = new int [n] ;//在堆申请空间,长度为 n的int类型数组,语法正确 (人工分配,人工回收)
int n; cin >> n; int a[n] ; // 定义数组时,数组长度为变量,C 语言正确,但 C++不支持!(如果可以申请是在栈空间申请)
3.已知二叉树先序序列、中序序列,求后序序列 或 已知二叉树后序序列、中序序列,求先序序列
tips :由先序序列可知第一个(由后序序列可知最后一个)为根结点,由中序序列(根结点必在中间)可区分根结点左右子树
eg.若二叉树先序序列:ACBEHDGF,中序序列:BCHEAGFD。则后序序列是?//BHECFGDA
-----> 由先序可知,A 是根结点,再由中序可知,BCHE 是左子树,GFD 是右子树;由先序可知,C 是左子树的根结点,再由中序可知,C 的左孩子为 B,C 的右子树是 HE.....
4.树的同构——给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。所以除了考虑对称同构,与原树相同也是同构。
