当我们应用统计方法对数据进行分析时,会发现许多分析方法如T检验、方差分析、相关分析以及线性回归等等,都要求数据服从正态分布或近似正态分布,正态分布在机器学习的重要性后期会讲述。上一篇文章用Q-Q图来验证数据集是否符合正态分布,本文首先介绍了偏度与峰度的定义,然后用偏度与峰度检测数据集是否符合正态分布,最后分析该检测算法的适用条件以及SPSS的结果分析。
1、 偏度与峰度
(1) 偏度(Skewness)
偏度衡量随机变量概率分布的不对称性,是相对于平均值不对称程度的度量,通过对偏度系数的测量,我们能够判定数据分布的不对称程度以及方向。
具体来说,对于随机变量X,我们定义偏度为其的三阶标准中心距:
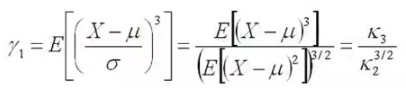
对于样本的偏度,我们一般记为SK,我们可以基于矩估计,得到有:

偏度的衡量是相对于正态分布来说,正态分布的偏度为0,即若数据分布是对称的,偏度为0。若偏度大于0,则分布右偏,即分布有一条长尾在右;若偏度小于0,则分布为左偏,即分布有一条长尾在左(如下图);同时偏度的绝对值越大,说明分布的偏移程度越严重。
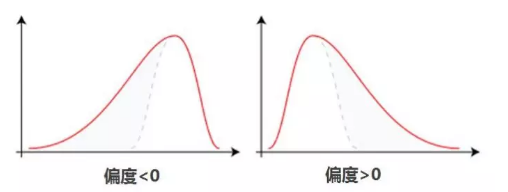
【注意】数据分布的左偏或右偏,指的是数值拖尾的方向,而不是峰的位置。
(2) 峰度(Kurtosis)
峰度,是研究数据分布陡峭或平滑的统计量,通过对峰度系数的测量,我们能够判定数据相对于正态分布而言是更陡峭还是平缓。比如正态分布的峰度为0,均匀分布的峰度为-1.2(平缓),指数分布的峰度为6(陡峭)。
峰度,定义为四阶中心距除以方差的平方减3。
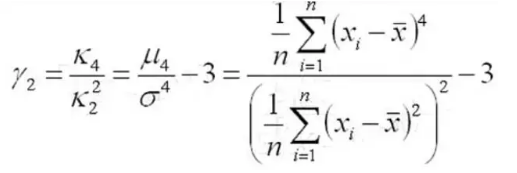
若峰度≈0,分布的峰态服从正态分布;
若峰度>0,分布的峰态陡峭(高尖);
若峰度<0,分布的峰态平缓(矮胖);

2、 正态性检验
利用变量的偏度和峰度进行正态性检验时,可以分别计算偏度和峰度的Z评分(Z-score)。
偏度Z-score = 偏度值 ÷偏度值的标准差
峰度Z-score = 峰度值 ÷峰度值的标准差
在α=0.05的检验水平下,偏度Z-score和峰度Z-score是否满足假设条件所限制的变量范围,若都满足则可认为服从正态分布,若一个不满足则认为不服从正态分布。
3、 正态性检验的适用条件
样本的增加会减小偏度值和峰度值的标准差,相应的Z-score会变大,最终会拒绝条件假设,会给正确判断样本数据的正态性情况造成一定的干扰。因此,当样本量小于100时,用偏度和峰度来判断样本的正态分布性比较合理。
4、 SPSS结果分析

峰度Z-score = 5.166/0.425 > Z(α),α=0.05;因此该特征不符合正态分布。
参考:
https://www.sohu.com/a/125526669_609133
https://www.sohu.com/a/140979052_489312
