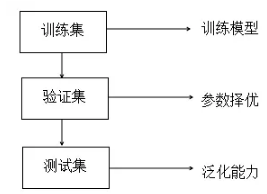
样本数据集在构建机器学习模型的过程中具有重要的作用,样本数据集包括训练集、验证集、测试集,其中训练集和验证集的作用是对学习模型进行参数择优,测试集是测试该模型的泛化能力。
正负样本数据集符合独立同分布是构建机器学习模型的前提,从概率角度分析,样本数据独立同分布是正负样本数据是从某一特定的数据分布随机抽取得到的,且正负样本的分布是不一样的。举例来说,若我们用非洲的西瓜作为训练集,然后用中国的西瓜作为测试集,则数据集可能不满足同分布这一前提;抛硬币是最简单的独立同分布;用较专业的学术用语来举例,若训练数据集符合正态分布,测试集符合均匀分布,那么数据集不满足独立同分布这一前提。
本文用Q-Q可以分析不同数据集是否为同一分布,且可以用Q-Q图来验证数据集是否符合正态分布。
一、累积分布函数与分位数
累计分布函数(CDF,Cumulative Distribution Function),顾名思义,是概率累计的过程。对某一变量X取值为x,则x的累计分布函数是所有小于x值的概率相加,公式如下:
分位数(quantile)的概念与累计分布函数类似,也是一种概率累计过程,如第一四分位数是累积分布概率达到0.25时所对应的变量值,第二四分位数是累计分布概率达到0.5时多对应的值,第三四分位数是累计分布概率达到0.75时对应的值,公式如下:
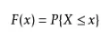
α代表累计概率,分位数为Zα:
P(X<=Zα) = α ;
二、Q-Q图定义
Q-Q是一种散点图,横坐标为某一样本的分位数,纵坐标为另一样本的分位数,横坐标与纵坐标组成的散点图代表同一个累计概率所对应的分位数。若散点图在直线y=x附近分布,则这两个样本是同等分布;若横坐标样本为标准正态分布且散点图是在直线y=x附近分布,则纵坐标样本符合正态分布,且直线斜率代表样本标准差,截距代表样本均值。

如上图左上角图为某一数据的累计概率分布函数,右上角为标准正态分布的累计概率分布函数,对上述两图取同一个累计概率值对应的分位数,绘制散点图,由图可知,数据符合正态分布,斜率和截距分别代表数据的标准差和均值。
QQ图中正态分布直线的推导:
若数据x是正态分布的,那么f(x)是一个正态分布的概率密度函数,根据正态分布的特性,数据x对应的标准正态分布函数的概率密度函数:
y =f((x-m)/std),其中m为样本均值,std为样本标准差
横坐标的数据分布是标准正态分布,概率密度函数为f(n),由QQ图定义可知两者是一一对应的,因此有:
(x-m)/std = n ;
即:x = n*std + m;
所以直线的斜率代表标准差,截距代表均值。
三、构建普通QQ图
普通QQ图用于评估两个数据集的分布的相似程度,如上节所说的,若散点图在直线y=x附近,则两个数据集的分布类似。普通QQ图与正态QQ图的不同点在于普通QQ图的横坐标是未知数据集的分位数,正态QQ图的横坐标是标准正态分布的分位数,其他步骤都一样。
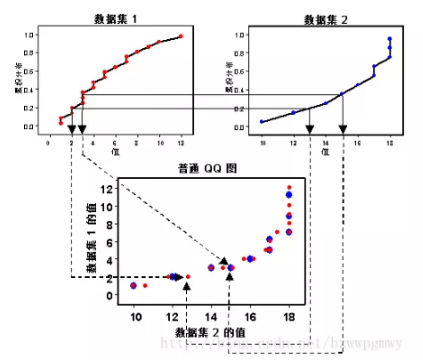
由上图可知,散点图没有接近一条直线,因此数据集1和数据集2来自不同的分布集。
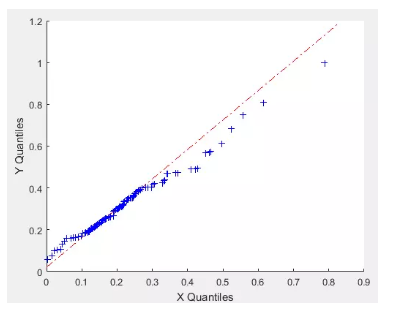
上图是本人所从事项目数据的普通QQ图,散点图接近一条直线,因此可以认为数据集是来自同一分布。
参考:https://blog.csdn.net/hzwwpgmwy/article/details/79178485
