CDQ分治----P4390 [BOI2007]Mokia 摩基亚

 

思路

看到这题目我直接想到了三值偏序，然后我就开始了不归之路

1.把操作按时间排序，就能离线操作了

2.首先读入的时候各个操作已经默认是按时间排序的了，所以不用考虑时间这一维

接着，操作分两种： （1）.添加住户（相当于是把这个点的权值加上一个a）

（2）.查询住户（查询的这个范围是个矩形）

所以自然就可以用归并排序+树状数组来解决了

其中最妙的一步在于将操作2中的给出的两个点进行扩展，扩展成4个点来进行操作，然后在归并排序的时候按照坐标x来排序，根据树状数组的性质来进行操作：

结合代码来讲一下

for (;tql!=3;){
    cin>>tql;
    if(tql == 1)R++,T[R].tt=R,cin>>T[R].x>>T[R].y>>T[R].z;
    if(tql == 2){
        int q=R;
        book[q]=1;
　　　　　int X1,X2,Y1,Y2;
　　　　  cin>>X1>>Y1>>X2>>Y2;
　　　　 R++;q=R;T[R].x=X1-1,T[R].y=Y1-1,T[R].tt=q,T[R].t=1;//待会在CDQ+树状数组中对应下图左上一块，因为在Case 2，3中被多减去了一次，所以要加上
　　　　 R++;T[R].x=X1-1,T[R].y=Y2,T[R].tt=q,T[R].t=2;//对应的是下图黄色的正方形右上点到最左上红点的区间
　　　　 R++;T[R].x=X2;T[R].y=Y1-1;T[R].tt=q,T[R].t=3;//对应的是黄色的正方形坐下点到最左上红点的区间（第2,3块区间要减去，因为我们只要黄色正方形的部分，但是我们在计算的时候算的是右下的点到红色左上点的整个面积，所以要减去）
　　　　 R++;T[R].x=X2;T[R].y=Y2;T[R].tt=q,T[R].t=4;//包含了最右下点到最左上红点这一整块的区间
　　　　//另外就是因为要处理边界的问题，所以会见到一些  "-1"的运算，因为我们计算的时候黄色正方形的四条边上包括的点也是要算进来的
　　　　//所以我们减去的时候就要注意不要把边上的点也删去了

    }
}

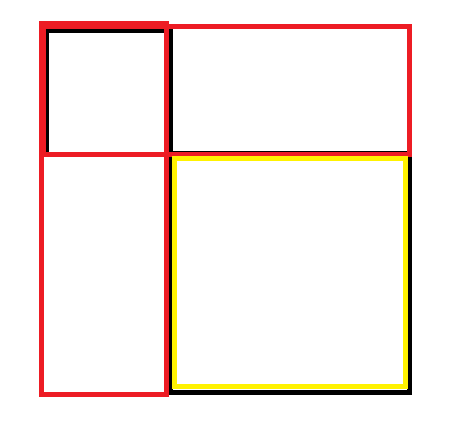
（见tql==2的情况）

（给拓展的四个点进行标记然后在后面计算答案）

if(T[t2].t == 1)tong[T[t2].tt]+=get(T[t2].y);//如果是左上点，因为被重复减了一次，所以要加上

if(T[t2].t == 2)tong[T[t2].tt]-=get(T[t2].y);//因为不是我们要求的区间，所以减去

if(T[t2].t == 3)tong[T[t2].tt]-=get(T[t2].y);//因为不是我们要求的区间，所以减去

if(T[t2].t == 4)tong[T[t2].tt]+=get(T[t2].y);//计算右下角的点到最左上红点的整个大区间

此处请自行脑补一个树状数组

CODE

#include <bits/stdc++.h>
using namespace std;
int c[2005001];
int tong[200001];
int w, tql, R = 0;
struct node {
    int x, y, z, t, tt;
} T[200001], p[200001];
int book[200005];
int lowbit(int x) { return x & (-x); }

int add(int x, int k) {
    while (x <= w) c[x] += k, x += lowbit(x);
    return 0;
}

int get(int x) {
    int total = 0;
    while (x > 0) total += c[x], x -= lowbit(x);
    return total;
}

int CDQ(int l, int r) {
    if (l == r)
        return 0;
    int mid = (l + r) >> 1;
    CDQ(l, mid);
    CDQ(mid + 1, r);
    int t1 = l, t2 = mid + 1;
    for (int i = l; i <= r; i++) {
        if (T[t1].x <= T[t2].x && t1 <= mid || t2 > r) {
            if (T[t1].t == 0)
            add(T[t1].y, T[t1].z);
            p[i] = T[t1], t1++;
        } 
        else {
            if (T[t2].t == 1)tong[T[t2].tt] += get(T[t2].y);
            if (T[t2].t == 2)tong[T[t2].tt] -= get(T[t2].y);
            if (T[t2].t == 3)tong[T[t2].tt] -= get(T[t2].y);
            if (T[t2].t == 4)tong[T[t2].tt] += get(T[t2].y);
            p[i] = T[t2], t2++;
        }
    }
    for (int i = l; i <= mid; i++)
        if (T[i].t == 0)
            add(T[i].y, -T[i].z);
    for (int i = l; i <= r; i++) T[i] = p[i];
    return 0;
}
int main() {
    cin >> tql >> w;
    R = 0;

    for (; tql != 3;) {
        cin >> tql;
        if (tql == 1)
            R++, T[R].tt = R, cin >> T[R].x >> T[R].y >> T[R].z;
        if (tql == 2) {
            int q;
            int X1, X2, Y1, Y2;
            cin >> X1 >> Y1 >> X2 >> Y2;
            R++;q = R;T[R].x = X1 - 1, T[R].y = Y1 - 1, T[R].tt = q,T[R].t = 1;/*待会在CDQ+树状数组中对应下图左上一块，因为在Case 2，3中被多减去了一次，所以要加上*/
            book[q]=1;
            R++;T[R].x = X1 - 1, T[R].y = Y2, T[R].tt = q,
            T[R].t = 2;  /*对应的是下图黄色的正方形右上点到最左上红点的区间*/
            R++;T[R].x = X2;T[R].y = Y1 - 1;T[R].tt = q,T[R].t =3;/*对应的是黄色的正方形坐下点到最左上红点的区间（第2,3块区间要减去，因为我们只要黄色正方形的部分，但是我们在计算的时候算的是右下的点到红色左上点的整个面积，所以要减去）*/
            R++;T[R].x = X2;T[R].y = Y2;T[R].tt = q, T[R].t = 4;/*包含了最右下点到最左上红点这一整块的区间*/
            /*另外就是因为要处理边界的问题，所以会见到一些  "-1"的运算，因为我们计算的时候黄色正方形的四条边上包括的点也是要算进来的
　　　　　　  所以我们减去的时候就要注意不要把边上的点也删去了*/
        }
    }
    CDQ(1, R);
    for (int i = 1; i <= R; i++)
        if (book[i] != 0)
        cout << tong[i] << endl;
    return 0;
}