概
作者通过普通的数据 (有 bias 的) 和少量的无偏数据来缓解大部分的 bias.
符号说明
- \(\mathcal{U}\), users;
- \(\mathcal{I}\), items;
- \(\mathcal{R}\), ratings;
- \(D_T = \{(u_k, i_k, r_k)\}_{1 \le k \le |D_T|}\), 有偏的数据集;
- \(D_U = \{(u_l, i_l, r_l)\}_{1 \le l \le |D_U|}\), 无偏的数据集;
- \(p_T(u, i, r)\), \(D_T\) 所对应的分布;
- \(p_U(u, i, r)\), \(D_U\) 所对应的分布;
- \(O_{ui} = 1\) 表示观测到 \(u,i\) 的交互;
动机
-
我们需要拟合一个模型 \(f_{\theta}(u, i)\) 得到 \(r_{u,i}\) 的一个估计 \(\hat{r}_{u, i}\), 特别地, 我们更希望通过如下的理想的无偏数据进行优化
\[L(f) = \mathbb{E}_{p_U} [\delta ( f(u, i), r_{u,i})], \]其中 \(\delta(\cdot, \cdot)\) 是某个损失函数;
-
然后在实际上, 我们所能获得的只是一部分有偏的数据 \(D_T\), 并通过如下的损失进行优化
\[\hat{L}_T(f) = \frac{1}{|D_T|} \sum_{k=1}^{|D_T|} \delta (f(u_k, i_k), r_k), \]而且通常
\[\mathbb{E}_{p_t}[\hat{L}_T(f)] \not = L(f); \] -
造成此情况的主要原因是现有的数据 \(D_T\) 往往是有偏的:
- Selection bias: 用户会有选择地打分, 比如一些用户只会给觉得特别好看的打分;
- Conformity bias: 用户往往有从众心理, 导致对一些打分不是很'客观' (\(p_T(r|u, i) \not= p_U(r|u, i)\));
- Exposure bias: 由于用户所看的电影也往往是在软件所推荐的结果中来的, 故 \(p_T(u, i) \not = p_U(u, i)\) 并非是一个随机的情况;
- Position bias: items 被推荐的顺序, 位置会影响每个 item 的曝光机会, 导致 \(p_T(u, i) \not = p_U(u, i)\), 此外, 倘若用户比较信赖推荐结果的话, 往往会导致 \(p_T(r|u, i) \not= p_U(r|u, i)\) 也不一致;
-
当这些 bias 产生的时候, 会导致 (从分布 shift 的角度):
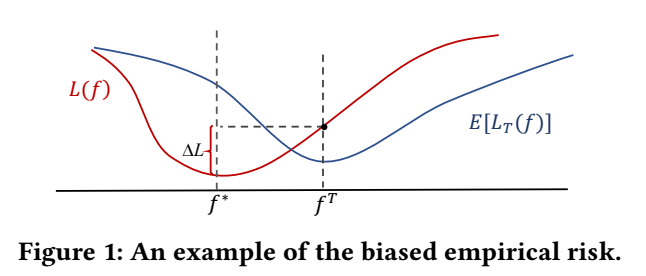
本文方法
- 由于数据的 bias 和本身量的有限, 作者认为 \(p_T\) 所在的支撑集 \(S_1\) 相比 \(p_U\) 的 \(S_1\cup S_0\) 是要小的:
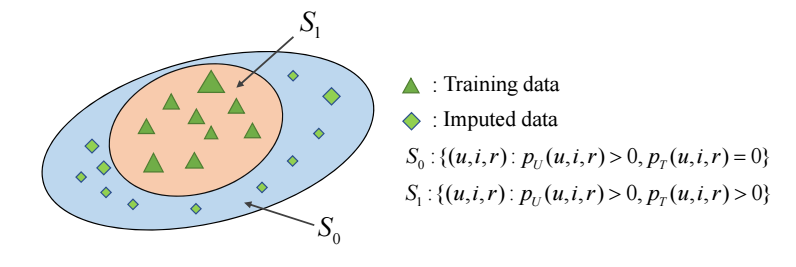
-
进行如下分解:
\[\begin{array}{ll} L(f) &= \mathbb{E}_{p_U} [\delta] \\ &= \sum_{u, i, r} p_U(u, i, r) [\delta(f(u, i), r_{u, i})] \\ &= \sum_{u, i, r \in S_1} [p_U(u, i, r) \delta(f(u, i), r_{u, i})] +\sum_{u, i, r \in S_0} [p_U(u, i, r) \delta(f(u, i), r_{u, i})] \\ &= \sum_{u, i, r \in S_1}[ p_T(u, i, r) \frac{p_U(u, i, r)}{p_T(u, i, r)} \delta(f(u, i), r_{u, i})] +\sum_{u, i, r \in S_0}[ p_U(u, i, r) \delta(f(u, i), r_{u, i})] \\ &= \mathbb{E}_{p_T} [\frac{p_U(u, i, r)}{p_T(u, i, r)} \delta(f(u, i), r_{u, i})] +\sum_{u, i, r}[ p_U(u, i, r) I(p_T(u, i, r) =0) \delta(f(u, i), r_{u, i})] \\ &= \mathbb{E}_{p_T} [\frac{p_U(u, i, r)}{p_T(u, i, r)} \delta(f(u, i), r_{u, i})] +\mathbb{E}_{p_U(u, i)} I(p_T(u, i) =0) [\sum_{r} p_U(r|u, i) \delta(f(u, i), r_{u, i})] \\ &= \mathbb{E}_{p_T} [\frac{p_U(u, i, r)}{p_T(u, i, r)} \delta(f(u, i), r_{u, i})] +\mathbb{E}_{p_U(u, i)} \Big \{ I(p_T(u, i) =0) \mathbb{E}_{p_U(r|u, i)} [\delta(f(u, i), r_{u, i})] \Big \}, \end{array} \]假设 \(\delta(\cdot, \cdot)\) 关于第二项是线性的 (比如交叉熵, 作者说 L1, L2 也可以 ?), 记
\[w^{(1)}(u, i, r) = \frac{p_U(u, i, r)}{p_T(u, i, r)}, \\ w^{(2)}(u, i) = \sum_{r} p_U(u, i, r) I(p_T(u, i, r) = 0), \\ m(u, i) = \mathbb{E}_{p_U(r|u, i)} [r_{u, i}], \]则
\[L(f) = \underbrace{\mathbb{E}_{p_T} [w^{(1)} \delta (f(u, i), r_{u, i})]}_{L_T} + \underbrace{\sum_{u, i} w^{(2)} \delta (f(u, i), m(u, i))}_{L_U}, \]可以注意到, \(L(f)\) 的第一部分可以用一般的 (在估计 \(w^{(1)}\) 的前提下)
\[\hat{L}_T = \frac{1}{|D_T|} \sum_{k=1}^{|D_T|} [w^{(1)} \delta (f(u_k, i_k), r_{u_k, i_k})] \]近似, 倘若我们还能估计出 \(w^{(2)}, m\), 那么我们第二部分也是可以计算的;
-
既然如此, 本文就将 \(\phi = \{w^{(1)}(u, i, r), w^{(2)} (u, i), m(u, i)\}_{u, i}\) 也作为可学习的参数来学习, 当然了, 直接学习很容易过拟合, 所以采用如下的方式:
\[w^{(1)}(u, i, r) = \exp(\varphi_1^T [x_{u} \circ x_{i} \circ e_r]) \\ w^{(2)}(u, i) = \exp(\varphi_2^T [x_{u} \circ x_{i} \circ e_{O_{ui}}]) \\ m(u, i) = \sigma(\varphi_3^T [e_{r_{ui}} \circ e_r]) \\ \]其中 \(x_u, x_i\) 是 \(u, i\) 的特征, \(e_r, e_{O_{u,i}}\) 是 one-hot 向量, \(\circ\) 表示向量拼接操作, \(\sigma\) 是激活函数, 比如 \(\tanh\);
-
至于参数的训练方式, 作者采用的是交替迭代 \(\theta, \phi\) 的方式:
- 通过 \(\hat{L}_T\) 临时 更新得到 \(\theta'\);
- 在 \(\theta'\) 的基础上更新 \(\varphi\);
- 在 \(\theta, \varphi\) 的基础上更新 \(\theta\).
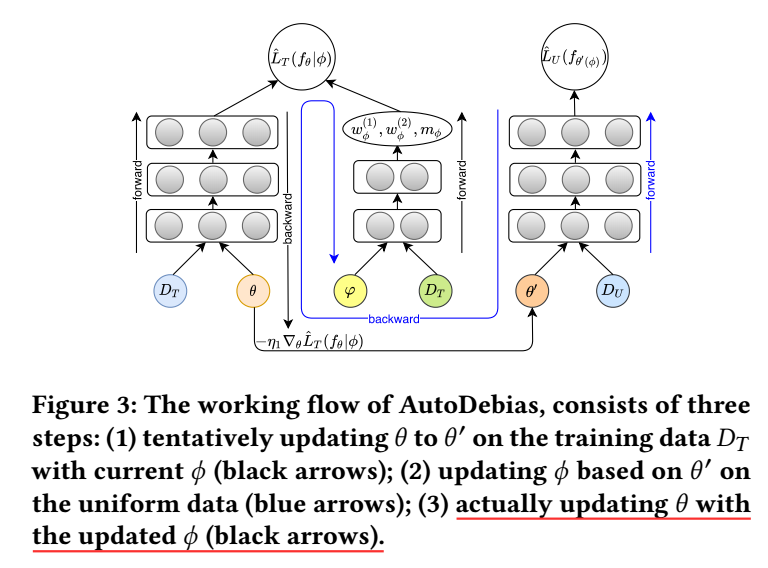
注: 关于公式的推导, 这里和论文的不同 (因为我按照论文的写法顺不下来), 虽然最后的结果是不影响的, 但是我觉得还是回看下论文确认一下比较好 !
注: 注意到优化 \(\hat{L}_U\) 需要无偏的损失, 所以作者的实验部分选的数据集也是带有这些无偏数据的, 这些无偏数据是狭隘, 指的是 item 采取一种随机的方式推荐给用户, 所以原则上 Selection bias, Conformity bias 等不能消除?
代码
[official]