The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks

目录

• 概
• 动机
• 算法
• 一些实验结果
  • MNIST + LeNet
  • CIFAR-10 + Conv + Dropout
  • CIFAR-10 + VGG|ResNet + lr decay + augmentation

Frankle J. and Carbin M. The lottery ticket hypothesis: finding sparse, trainable neural networks. In International Conference on Learning Representations (ICLR), 2019.

概

网络稀疏性中的 Lottery Ticket Hypothesis.

动机

在此之前的网络的 pruning 通常采取这样的操作:

• 一个较大的网络 \(f(\cdot; \theta)\);
• 进行一次完整的训练;
• 重复如下操作直到满足需要的稀疏率:

  1. 对 \(f(\cdot; \theta)\) 进行裁剪, 得到

     \[f(\cdot; m_i \odot \theta), \]

     其中 \(m_i\) 是 mask;

  2. 对 \(f(\cdot; m_i \odot \theta)\) 进行训练, 恢复一些 accuracy;

显然这个流程是十分耗时的. 现在的问题是, 能不能先裁剪, 再训练呢? 即

• 对网络 \(f(\cdot; \theta)\) 进行裁剪 (或许也是迭代式的) 得到一个高度稀疏的网络 \(f(\cdot; m \odot \theta)\);
• 进行一次完整的训练.

但是实践下来, 这样子做通常难以训练, accuracy 也很糟糕. 本文严格来说不是解决这个问题的, 只是经验性地证明:

1. 假设前向网络 \(f(\cdot; \theta)\) 初始化为 \(\theta_0\);
2. 采用算法 \(\mathcal{A}\) 进行训练集 \(\mathcal{D}\) 上训练 \(T\) 次在验证集上到达最小损失 \(l\), 且测试 accuracy 为 \(\rho\);
3. 则存在 mask \(m \in \{0, 1\}^{|\theta|}, \|m\|_0 \ll |\theta|\), 网络 \(f(\cdot; m \odot \theta)\) 初始化为 \(m \odot \theta_0\);
4. 采用算法 \(\mathcal{A}\) 进行训练集 \(\mathcal{D}\) 上训练 \(T'\) 次达到验证损失最小 \(l'\), 且测试 accuracy 为 \(\rho'\);
5. 则 \(T' \le T, \rho' \ge \rho\), 即能够用更少的时间获得更好的结果.

一般的 Lottery Ticket Hypothesis 为:

A randomly-initialized, dense neural network contains a subnetwork that is initialized such that—when trained in isolation—it can match the test accuracy of the original network after training for at most the same number of iterations.

算法

作者设计了一个算法去寻找这样的一个 winning ticket:

1. 随机初始化网络 \(f(x; \theta)\) 为 \(\theta_0\);
2. 训练 \(T\) 次得到参数 \(\theta_T\);
3. 裁剪掉其中 \(p\%\) 的 smallest-magnitude 权重, 得到 mask \(m\);
4. 得到网络 \(f(x; m \odot \theta_T)\) 并重新初始化为 \(f(x; m \odot \theta_0)\) (注意, 这里的 \(\theta_0\) 和 1 中的 \(\theta_0\) 必须是同一个 \(\theta_0\) !);
5. 对 \(f(x; m \odot \theta_0)\) 重复 2,3,4 操作直到满足需要的稀疏率.

需要注意的是, 如果设置的稀疏率过于低, 所找到的 ticket 的性能就比不上原先的网络 \(f(x; \theta_T)\) 了.

一些实验结果

MNIST + LeNet

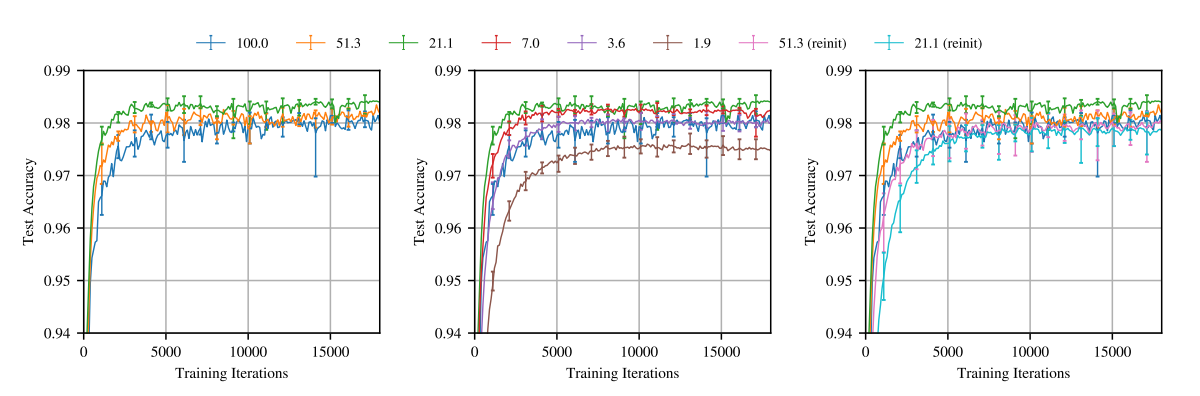
如上图所示:

1. 稀疏率为 \(21.1\%\) 的网络明显优于原先的 \(100\%\) 的网络;
2. 但是这个性质, 倘若在第 4 步 \(\theta\) 重新初始化为 \(\theta_0' \not= \theta_0\), 就会失效.

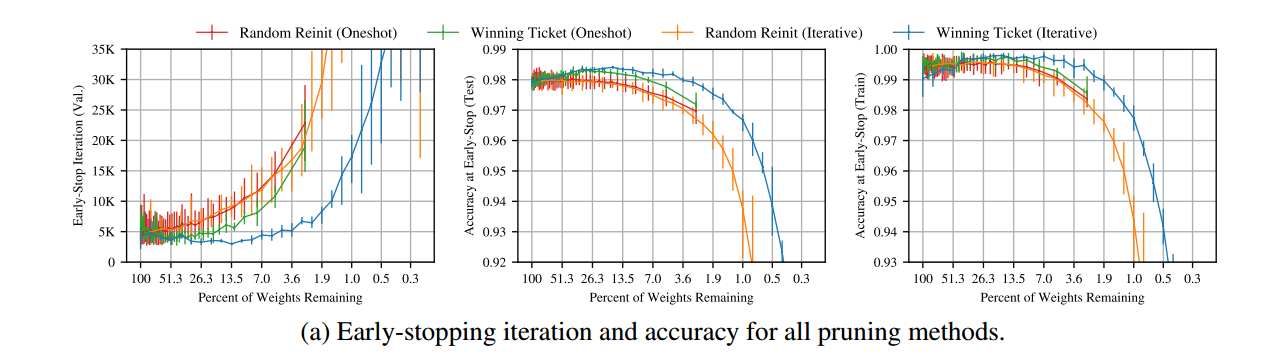
此外稀疏化后的网络训练速度更快 !

CIFAR-10 + Conv + Dropout

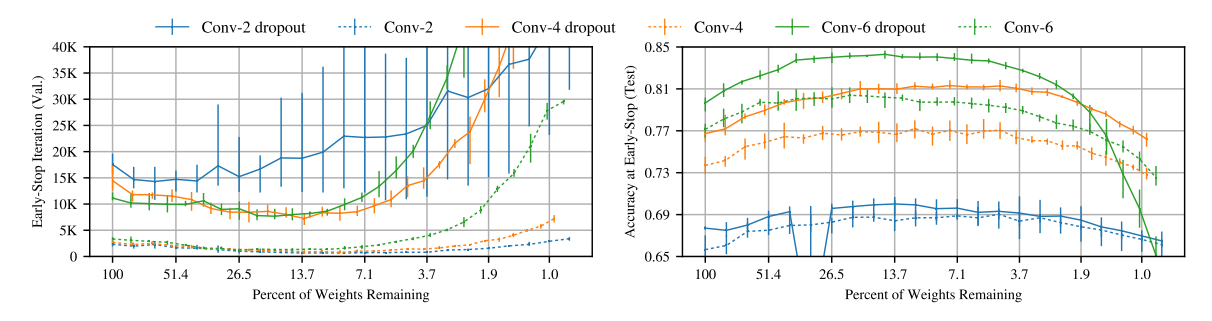
该算法找到的 winning ticket 对于卷积网络和常用的 dropout 也同样适用.

CIFAR-10 + VGG|ResNet + lr decay + augmentation

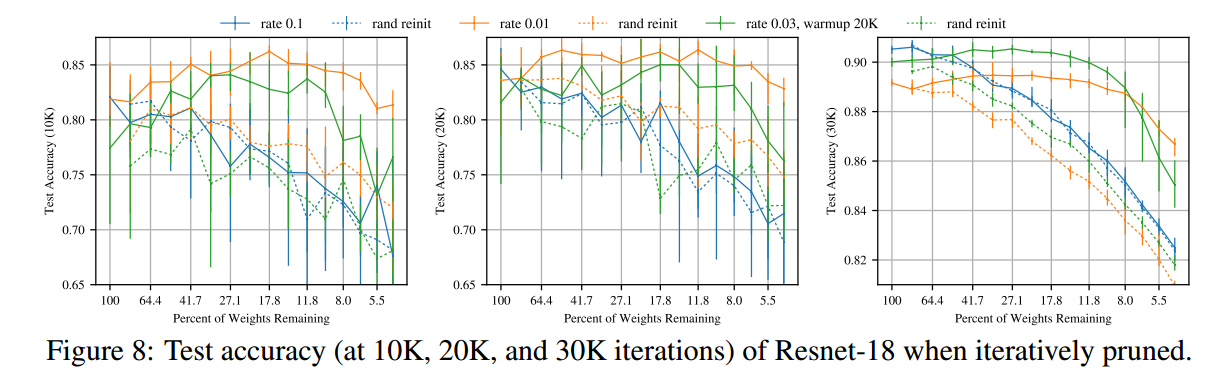
这里作者在更深的网络上测试, 并套用了更多的 tricks: lr decay 和 data augmentaton. 作者发现对于这种情况需要两种特殊的操作:

1. Global pruning: 即裁剪的时候是在整体而非逐层的裁剪 (之前的逐层是因为每层之间的参数量相差不大);
2. 如果初始的学习率很大, 那么需要通过 warmup 令学习率从 0 爬升到初始学习率.