概
有关 POI (Point-of-Interest) 的推荐, 利用图网络提取特征, 利用 TIE (Total Indirect Effect) 来消除 geographical bias (即用户所选择的场所, 可能不是纯兴趣导向的, 而很大程度受距离远近的影响).
符号说明
- \(\mathcal{U}\), users;
- \(\mathcal{P}\), POIs;
- \(\mathcal{O}^+ = \{(u, p)\}\), 表示 \(u\) 曾经访问过 \(p\);
除了上面的传统的数据对象外, 本文所设计的数据集还包括:
- \(\mathcal{E}\), 城市中的各种 entity (\(\mathcal{P} \subset \mathcal{E}\));
- \(\mathcal{R}\), 场所中所满足的一些关系.
举个例子,
(Apple Store East Nanjing Road, BrandOf, Apple)
这表示, POI 'Apple Store East Nanjing Road' 的 brand 是 entity 'Apple'.
下面作者所提供的一些关系:
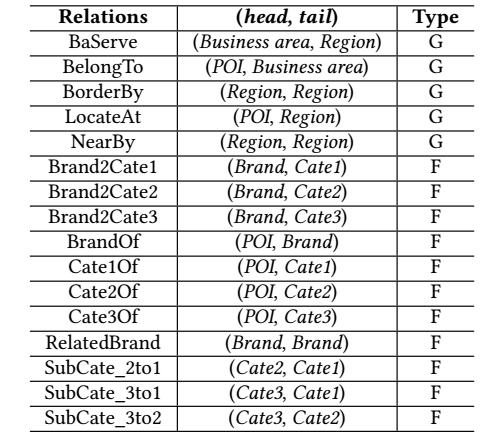
分为 geographical (地理上的关系) 和 functional (功能上的关系) 两类.
流程
-
为每个 user \(u_i\) 分配 embeddings:
\[\bm{u}_{i, g}, \bm{u}_{i, f} \in \mathbb{R}^d, \]分别表示 geographical 和 functional 上的 embeddings.
类似地, 为 POI entitiy \(p_j\) 和 非 POI entity \(v_k\) 也分配:\[[\bm{p}_{j, g}, \bm{p}_{j, f}], \: [\bm{v}_{k, g}, \bm{v}_{k, f}]; \] -
对于关系图 \(\mathcal{R}_g, \mathcal{R}_f\) 的第 \(j\) 个关系赋予 embedding:
\[\bm{r}_{j, g}, \bm{r}_{j, g}; \] -
作者认为, user, POI 之间的交互主要受各种目的 (intents) 影响, 作者分别建模 geographical 和 functional 的 intents \(\mathcal{I}_g, \mathcal{I}_f\), 其中第 \(i\) 个 intent 定义为:
\[\bm{e}_{i, g} = \sum_{r_{j, g} \in \mathcal{R}_g} \alpha(i, j) \bm{r}_{j, g}, \]其中
\[\alpha(i, j) = \frac{s_{ij}}{\sum_{r_{k, g} \in \mathcal{R}_g \exp(s_{ik})}}, \]\(s_{ij}\) 是 intent \(i\) 和关系 \(j\) 之间的一个权重, 是可训练的参数;
-
第 \(l\) 层, 通过下列方式进行聚合:
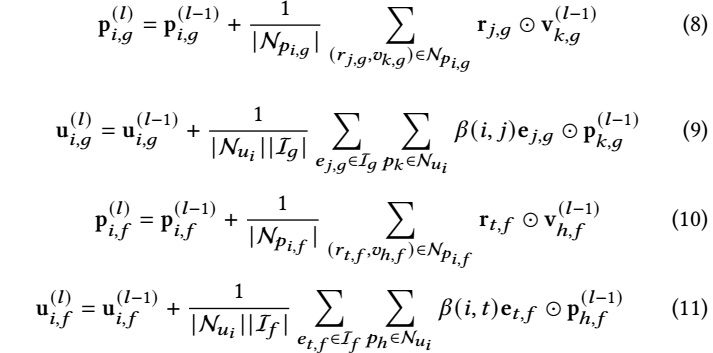
其中 (话说 \(\beta(i, j)\) 和 \(l\) 无关?)
\[\beta(i, j) = \frac{\bm{e}_{j, g}^T \bm{u}_{i, g}^{(0)}}{\sum_{e_{t, g} \in \mathcal{I}_g} \exp(\bm{e}_{t, g}^T \bm{u}_{i, g}^{0})}; \] -
最后得到 embeddings:
\[\bm{u}_i = \frac{1}{2}(\bm{u}_{i, g}^{(l)} + \bm{u}_{i, f}^{(l)}), \\ \bm{p}_i = \frac{1}{2}(\bm{p}_{i, g}^{(l)} + \bm{p}_{i, f}^{(l)}). \\ \]
Counterfactual Learning
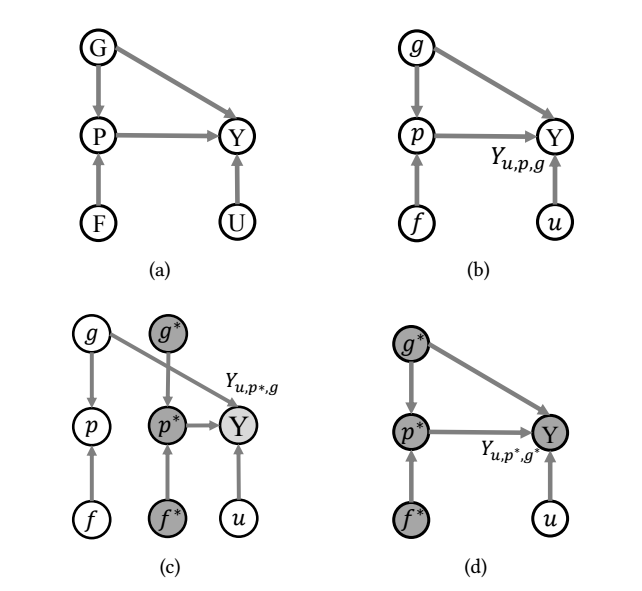
作者认为, POI 推荐是流程是符合 (a) 这种因果模型的, 即最终的 \(Y\) 收到地理位置 G, 场所 P, 和用户 U 三者的直接影响. 但是作者认为, \(G \rightarrow Y\) 会导致推荐的结果很大程度的受到地理位置的影响, 而不是纯依赖兴趣.
Q: 个人认为, \(G \rightarrow Y\) 作为推荐来说没啥问题, 毕竟大家一般来说都不太愿意走太远吧.
所以作者实际上希望推荐的依据尽可能不直接受地理位置的影响, 这里需要注意的是, 不直接受不代表不受, 因为即使去掉了 \(G \rightarrow Y\), 也会通过 \(G \rightarrow P \rightarrow Y\) 间接影响 (比如地域位置会影响店铺的规模). 作者希望通过 TIE (Total Indirect Effect) 来估计:
受 [4, 22, 32] (没看) 的启发,
而
优化
-
普通的 BPR 损失用于提高 (\(\bm{u}_i, \bm{p}_j\)) 的精度:
\[\mathcal{L}_{F} = \sum_{(u_i, p_j, p_k) \in \mathcal{O}} -\ln \sigma(Y_{u_i, p_j} - Y_{u_i, p_k}), \]其中 \(\mathcal{O} = \{(u_i, p_j, p_k) : (u_i, p_j) \in \mathcal{O}^+, (u_i, p_k) \in \mathcal{O}^{-}\}\);
-
作者希望在 counterfactual world 中 \(Y_{u_i, p_j^*, g_j}\) 也具备预测能力, 而 \(Y_{u_i, p_j^*} = \mathbb{E} (Y_{u_i, P}) = Y_{u_i, p_k^*}\), 故实际上是优化如下的损失:
\[\mathcal{L}_{C} = \sum_{(u_i, p_j, p_k) \in \mathcal{O}} -\ln \sigma(Y_{u_i, g_j} - Y_{u_i, g_k}). \] -
最后是这些损失的一些组合, 还有一些用于解耦 embeddings 的正则项这里没写, 感兴趣的可以回看原文.
注: 对于 \(\mathcal{L}_C\) 我其实是不解的, 甚至我可能直接会用 \(\hat{y}_{u_i, p_j}\) 来 BPR. 我感觉这个样子可能会导致 \(Y_{u_i, p_j^*, g_j}\) 不具备预测能力, 反而容易导致 \(G\) 混入 \(P\) 中? 换言之 \(\mathcal{L}_C\) 只是为了 NDE 确实的表达为 NDE.