概
利用 GAN 伪造用户以及行为来使得推荐模型倾向于某种给定的 item (打分矩阵限定).
主要内容
符号说明
- \(\bm{U}\), real users;
- \(\bm{V}\), item;
- \(\bm{X} \in \mathbb{R}^{|\bm{V}| \times |\bm{U}|}\), 打分矩阵;
- \(\bm{U}_v:= \{u \in \bm{U}: \: x_{v, u} \not = 0\}\)
- \(\bm{V}_u:= \{v \in \bm{V}: \: x_{v, u} \not = 0\}\)
- \(\bm{U}'\), 伪造的用户;
- \(\bm{S}\), 目标 items, 即希望推荐系统偏向的目标 items;
- \(A = |\bm{U}'|\), 伪造的用户数量;
- \(P\), 伪造的用户的数据的打分的数量, 即 \(|\bm{V}_{u'}| = P\);
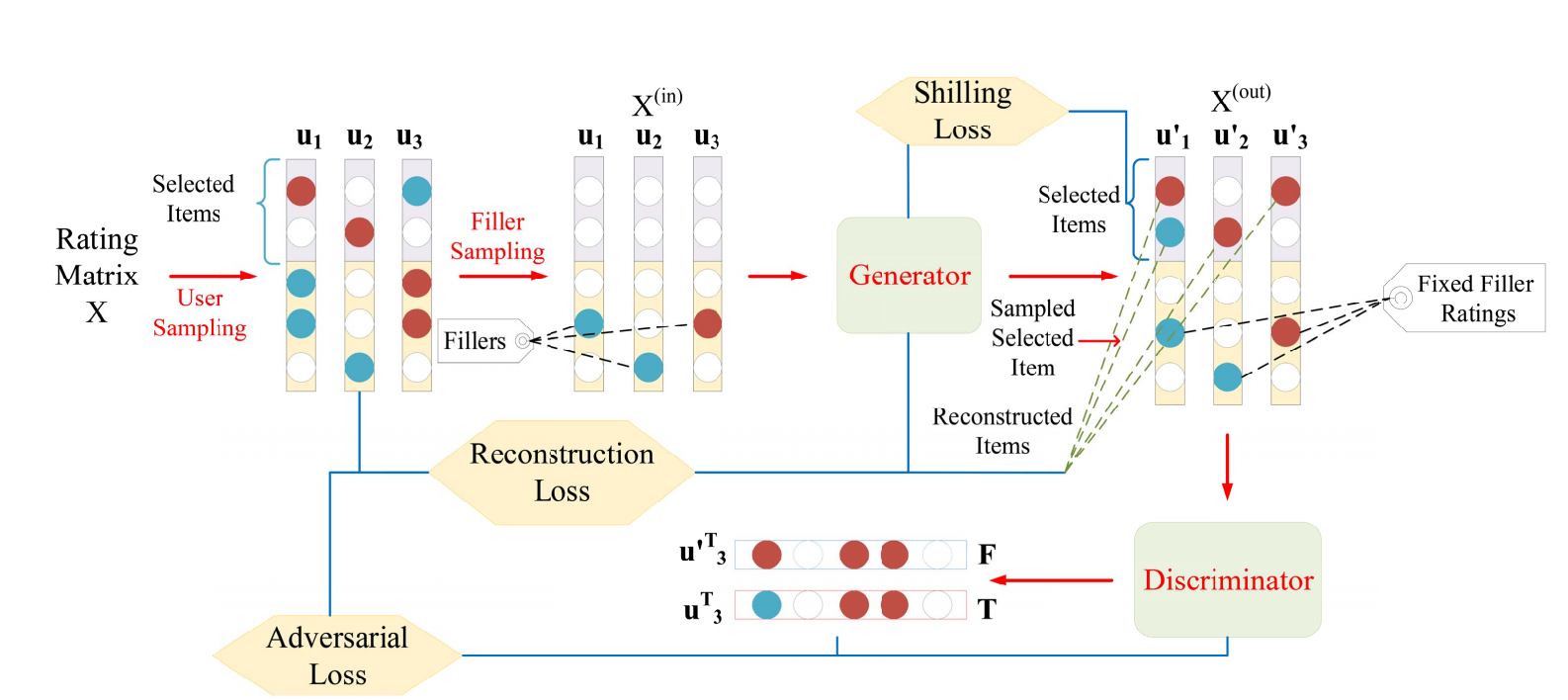
流程
- 从真实 users \(\bm{U}\) 中均匀采样得到 \(\bm{U}'\) (训练的时候似乎并不要求 \(|\bm{U}'| = A\)), 并记所对应的子打分矩阵为 \(\bm{X}^{(sub)} \in \mathbb{R}^{|\bm{V}| \times |\bm{U}|}\)作为模板. 并要求 \(|\bm{V}_{u'}| \ge P\);
- 构造矩阵 \(\bm{X}^{(in)}\), 其中元素要么为 \(\bm{X}_{v, u'}\) 或 \(0\) (即此时表示未观测); 文中提供了四种缺失采样的方法, 比如:
- Sample by Rating:
\[P(X_{v, u'}^{(in)} \not = 0) = \frac{\bar{r}_v}{\sum_{v \in \bm{V}_u} \bar{r}_v};
\]
- Sample by Popularity:
\[P(X_{v, u'}^{(in)} \not = 0) = \frac{|\bm{U}_v|}{\sum_{v \in \bm{V}_u} |\bm{U}_v|};
\]
- 通过 Generator 补全 \(S\) items 的打分情况, 得到 \(X^{(out)}\);
- 改不全后的矩阵首先需要满足和原有的真实打分矩阵相似, 通过重构损失来实现:
\[\tag{1}
\mathcal{L}_{recon} = \mathbb{E}_{u' \sim \bm{U}'} \sum_{j \in S} (\bm{X}_{j, u'}^{(out)} - \bm{X}_{j, u'})^2, \: \bm{X}^{(out)} = G(X^{(in)}; \theta);
\]
- 同时它需要骗过判别器 \(D(\cdot; \phi)\), 通过如下损失实现:
\[\tag{2}
\min_{\theta} \max_{\phi} H(G, D) = \mathbb{E}_{u \in \bm{U}} [\log D(\bm{x}_u; \phi)] + \mathbb{E}_{z \sim p_{\theta}} [\log (1 - D(z; \phi))];
\]
- 同时, 需要满足其能够使得推荐系统对 \(S\) 的 items 有偏, 故
\[\tag{3}
\mathcal{L}_{shill} = \mathbb{E}_{u' \sim \bm{U}'} \sum_{j \in \bm{S}} (X_{j, u'}^{(out)} - Q)^2,
\]
其中 \(Q\) 为 \(\bm{X}\) 中的最高分.
注: 个人感觉 (1) (3) 是冲突的, 而且仅凭 (3) 能否真的骗过推荐系统存疑.