概
其实看到推荐系统结合AutoEncoder, 我的第一反应是通过encoder提取特征, 然后利用注入内积的方式来计算得分. 没想到这里是直接预测得分.
主要内容
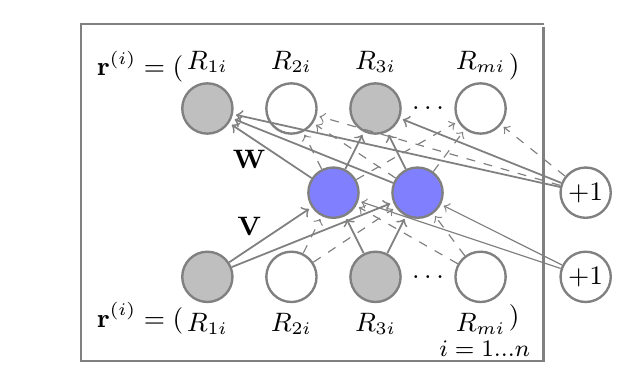
训练
对于得分矩阵 \(R \in \mathbb{R}^{m \times n}\), 每一行:
\[\bm{r}^{(u)} = (R_{u1}, \cdots, R_{un}) \in \mathbb{R}^n
\]
表示一个用户的打分, 每一列
\[\bm{r}^{(i)} = (R_(1i), \cdots, R_{mi}) \in \mathbb{R}^m
\]
表示一个物品的得分. 当然, \(R\)是一个稀疏的矩阵, 我们希望通过自编码预测这些缺失的元素:
\[\hat{\bm{r}} := h(\bm{r};\theta) = f(W g(V\bm{r} + \bm{\mu}) + \bm{b}),
\]
这个自编码的输入可以是\(\bm{r}^{(u)}\) (user-based) 或者 \(\bm{r}^{(i)}\) (item-based). 我们希望通过下式来使得预测更加准确:
\[\min_{W, V, \bm{\mu}, \bm{b}}\: \sum_{\bm{r}} \|\bm{r} - h(\bm{r}; \theta)\|_{\mathcal{O}}^2 + \frac{\lambda}{2} \cdot (\|W\|_F^2 + \|V\|_F^2),
\]
其中\(\|\cdot\|_{\mathcal{O}}\)表示仅非缺失(可观测)元素之间进行操作.
预测
我们可以通过:
\[\hat{R}_{ui} = (h(\bm{r}^{(i)}; \theta))_u
\]
或
\[\hat{R}_{ui} = (h(\bm{r}^{(u)}; \theta))_i,
\]
这取决于你选择item-based或者user-based的模型.
疑问
这个怎么冷启动呢? 模型的输入的维度都是固定的.