概
本文介绍了一种Normalizing FLow, 利用Householder变换.
主要内容
我们一般假设
[q_{phi} (z|x) = mathcal{N}(z| mu(x), sigma^2(x)),
]
但是常被人诟病的一点就是这个假设太粗暴简单了.
我们知道一个服从正态分布的随机变量(z)经过一个线性变化依旧是服从正态分布, 即
[Uz sim mathcal{N}(Umu(x), U mathrm{diag}(sigma^2(x))U^T).
]
倘若(U)是正交矩阵, 则(q(z_1) = q(z)), 则我们即让让分布更加灵活, 但不让计算变得复杂, 这种特殊的normalizing flow 是 volume preserving flow.
因为任意的正交矩阵都能够表示成
[U = H_K H_{K-1} cdots H_1,
]
(H)是形如(I - c cdot v v^T)的矩阵.
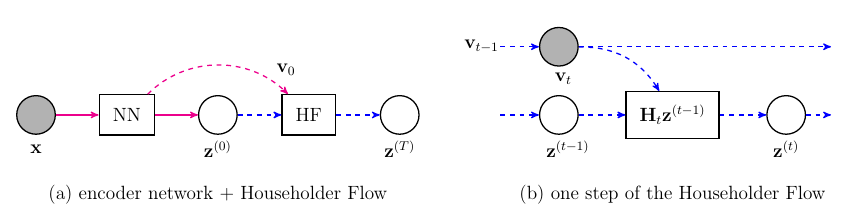
所以本文的设想是:
- Encoder 输出(z^0, v^0);
- 通过(v^0)构造(H_0)
[H_0 = (I - 2 frac{v_0v_0^T}{|v_0|^2_2});
]
- 得到(z^1 = H_0 z^0);
- 利用一个新的网络得到(v^1 = f_1(v_0));
- 以此类推, 得到最后的(z^T).
这就是整个flow.