Representation Learning with Contrastive Predictive Coding

目录

• 概
• 主要内容
  • 从具有序的数据讲起
  • Contrastive Predictive Coding (CPC)
  • 图片构建序

Den Oord A V, Li Y, Vinyals O, et al. Representation Learning with Contrastive Predictive Coding.[J]. arXiv: Learning, 2018.

Henaff O J, Srinivas A, De Fauw J, et al. Data-Efficient Image Recognition with Contrastive Predictive Coding[J]. arXiv: Computer Vision and Pattern Recognition, 2019.

@article{den oord2018representation,
title={Representation Learning with Contrastive Predictive Coding.},
author={Den Oord, Aaron Van and Li, Yazhe and Vinyals, Oriol},
journal={arXiv: Learning},
year={2018}}

@article{henaff2019data-efficient,
title={Data-Efficient Image Recognition with Contrastive Predictive Coding},
author={Henaff, Olivier J and Srinivas, Aravind and De Fauw, Jeffrey and Razavi, Ali and Doersch, Carl and Eslami, S M Ali and Den Oord, Aaron Van},
journal={arXiv: Computer Vision and Pattern Recognition},
year={2019}}

概

与其说是无监督, 不如用表示学习或者特征提取更为贴切. 感觉监督学习的一个瓶颈就是, 你直接告诉了神经网络它应该到达的终点, 那么它就会找一条最容易的路子去, 所以在训练中, 可以发现训练的精度很快就能达到100%, 而在测试集上的精度就差强人意了. 当然, 这错不在网络, 毕竟它已经尽可能地完成了我们交代给他的任务, 困难在于, 我们自己不知道该如何给这种兼顾泛化性的任务下达准确的定义(平移不变, 旋转不变等等只是泛化的冰山一角).
而表示学习的工作实际上就是比简单的分类损失等更具打磨的空间, 不同的先验知识可以融入其中. 这篇论文的观点就是, encoder提取的特征应当具有可预测性, 也就是说, 只有能够预测别的特征的才是好特征. 当然, 这个是对具有序(时域或者空间)的数据有意义, 对于图片可以认为构造这种数据, 个人认为这才是有趣的地方.

主要内容

从具有序的数据讲起

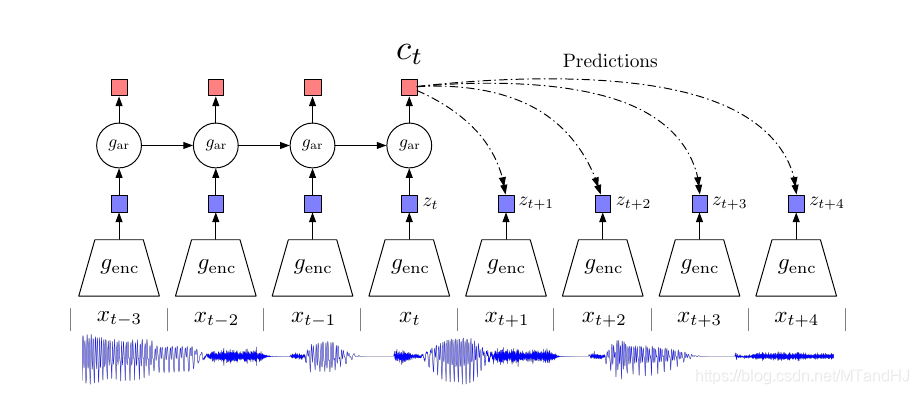
如上图, 在不同的时间点, 有数据(x_t), 其经过第一个encoder (g_{mathrm{enc}})得到隐变量(特征表示)(z_t). 到此打住, 如果是以前, 那可能再来一个decoder, 然后希望解码后数据和原始数据能够吻合. 不过作者认为, 这种方式有点太过勉强了, 其实一个好的特征并不是既低维度(高能量密度)又能够藏住大部分的信息, 一个好的特征应该是抓住最最最主要的信息, 如果是用于分类, 那就是抓住最具有区分度的信息(虽然这个很难下准确的定义).
作者的做法是, 将(z_i, ile t)作为输入, 构造一个回归模型(g_{mathrm{ar}})(比如用RNN), 得到一个实际上具有之前数据信息的一个特征表示(c_t). 作者希望利用(c_t)来预测之后的(x_{t+1},ldots, x_{t+k},ldots), 或者(z_{t+1},ldots, z_{t+k},ldots), 自然最好的是有一个条件概率模型(p(x_{t+k}|c_t)), 然后最大化互信息

[ ag{1} I(x;c)=sum_{x,c} p(x,c)log frac{p(x|c)}{p(x)}. ]

Contrastive Predictive Coding (CPC)

作者并没有打算构建条件概率模型(感觉这样就像VAE一样需要超多假设了), 只是用

[ ag{3} f_k(x_{t+k}, c_t)=exp(z_{t+k}^TW_kc_t), ]

来衡量二者的关系, 可以把(W_kc_t)看成是一个预测(hat{z}_{t+k}).

接下来就要用到对比学习的概念了, 文中说是利用了负样本采样, 但是我用负样本采样的那个推导实在推不出来他的函数, 但是是有一点类似的(感觉只是套用了负采样这个思想?). 即从(p(x_{t+k}|c_t))中采样正样本(x_{t+k}), 从一般的分布(p(x))中采样N-1个负样本(x_j), 然后最小化下式

[ ag{4} mathcal{L}_N=- mathbb{E}_X [log frac{f_k(x_{t+k},c_t)}{sum_{x_j in X} f_k(x_j,c_t)}]. ]

其中(X={x_1,ldots, x_N})(注, 这里(X)是固定的, 已知的).

把(frac{f_k(x_i,c_t)}{sum_{x_j in X} f_k(x_j,c_t)})看成是第(i)个采样点是正样本的概率(hat{p}_i,i=1, ldots,N), 则上面的式子实际上就是一个交叉熵

[mathcal{L}_N = -sum_{i=1}^N p_i log hat{p}_i, ]

故令损失最小的概率为(hat{p}_i=p_i:=p(d=i|X, c_t)), 即正样本在第(i)个位置的概率. 又

[egin{array}{ll} p(d=i|X, c_t) & = frac{p(x_i|c_t) prod_{l ot= i} p(x_l)}{sum_{j=1}^N p(x_j|c_t)prod_{l ot= j}p(x_j)} \ &= frac{frac{p(x_i|c_t)}{p(x_i)}}{sum_{j=1}^Nfrac{p(x_j|c_t)}{p(x_j)} }. end{array} ]

也就是说, 此时

[f_k(x_{t+k},c_t) propto frac{p(x_{t+k}|c_t)}{p(x_{t+k})}. ]

图片构建序

如图所示, 一张256x256的图片, 均匀分成7x7张, 每张大小为64x64, 两者最多有50%的重叠部分. 从上到下, 从左往右, 依次可以对其排序, 用前几行的patches出来的(z)来预测后面的(z).

疑问: 这个负样本的采样空间, 是一个图片所有的patches还是一个batch的所以的patches呢?