@article{mroueh2017mcgan:,
title={McGan: Mean and Covariance Feature Matching GAN},
author={Mroueh, Youssef and Sercu, Tom and Goel, Vaibhava},
journal={arXiv: Learning},
year={2017}}
概
利用均值和协方差构建IPM, 获得相应的mean GAN 和 covariance gan.
主要内容
IPM:
当(mathscr{F})是对称空间, 即(fin mathscr{F} ightarrow -f in mathscr{F}),可得
Mean Matching IPM
其中(|cdot |_p)表示(ell_p)范数, (Phi_w)往往用网络来表示, 我们可通过截断(w)来使得(mathscr{F}_{v,w,p})为有界线性函数空间(有界从而使得后面推导中(sup)成为(max)).

其中
最后一个等式的成立是因为:
又(| cdot |_p)的对偶范数是(|cdot|_q, frac{1}{p}+frac{1}{q}=1).
prime
整个GAN的训练过程即为
其中
估计形式为
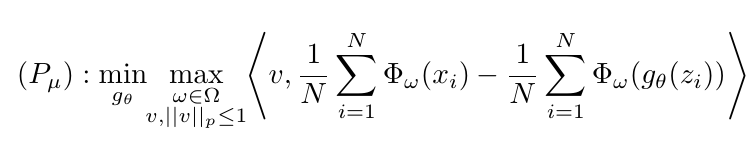
dual
也有对应的dual形态
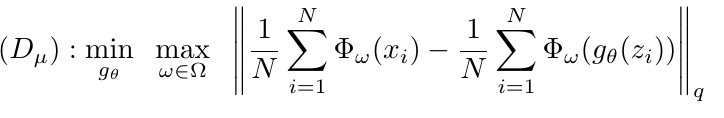
Covariance Feature Matching IPM
等价于
并有

其中([A]_k)表示(A)的(k)阶近似, 如果(A = sum_i sigma_iu_iv_i^T), (sigma_1ge sigma_2,ldots), 则([A]_k=sum_{i=1}^k sigma_i u_iv_i^T). (mathcal{O}_{m,k} := {M in mathbb{R}^{m imes k} | M^TM = I_k }), (|A|_*=sum_i sigma_i)表示算子范数.
prime
其中
采用下式估计

dual
注: 既然(Sigma_w(mathbb{P}_r) - Sigma_w(mathbb{P}_{ heta}))是对称的, 为什么(U ot =V)? 因为虽然其对称, 但是并不(半)正定, 所以(v_i=-u_i)也是有可能的.
算法



代码
未经测试.
import torch
import torch.nn as nn
from torch.nn.functional import relu
from collections.abc import Callable
def preset(**kwargs):
def decorator(func):
def wrapper(*args, **nkwargs):
nkwargs.update(kwargs)
return func(*args, **nkwargs)
wrapper.__doc__ = func.__doc__
wrapper.__name__ = func.__name__
return wrapper
return decorator
class Meanmatch(nn.Module):
def __init__(self, p, dim, dual=False, prj='l2'):
super(Meanmatch, self).__init__()
self.norm = p
self.dual = dual
if dual:
self.dualnorm = self.norm
else:
self.init_weights(dim)
self.projection = self.proj(prj)
@property
def dualnorm(self):
return self.__dualnorm
@dualnorm.setter
def dualnorm(self, norm):
if norm == 'inf':
norm = float('inf')
elif not isinstance(norm, float):
raise ValueError("Invalid norm")
p = 1 / (1 - 1 / norm)
self.__dualnorm = preset(p=p, dim=1)(torch.norm)
def init_weights(self, dim):
self.weights = nn.Parameter(torch.rand((1, dim)),
requires_grad=True)
@staticmethod
def _proj1(x):
u = x.max()
if u <= 1.:
return x
l = 0.
c = (u + l) / 2
while (u - l) > 1e-4:
r = relu(x - c).sum()
if r > 1.:
l = c
else:
u = c
c = (u + l) / 2
return relu(x - c)
@staticmethod
def _proj2(x):
return x / torch.norm(x)
@staticmethod
def _proj3(x):
return x / torch.max(x)
def proj(self, prj):
if prj == "l1":
return self._proj1
elif prj == "l2":
return self._proj2
elif prj == "linf":
return self._proj3
else:
assert isinstance(prj, Callable), "Invalid prj"
return prj
def forward(self, real, fake):
temp = (real - fake).mean(dim=1)
if self.dual:
return self.dualnorm(temp)
elif not self.training and self.dual:
raise TypeError("just for training...")
else:
self.weights.data = self.projection(self.weights.data) #some diff here!!!!!!!!!!
return self.weights @ temp
class Covmatch(nn.Module):
def __init__(self, dim, k):
super(Covmatch, self).__init__()
self.init_weights(dim, k)
def init_weights(self, dim, k):
temp1 = torch.rand((dim, k))
temp2 = torch.rand((dim, k))
self.U = nn.Parameter(temp1, requires_grad=True)
self.V = nn.Parameter(temp2, requires_grad=True)
def qr(self, w):
q, r = torch.qr(w)
sign = r.diag().sign()
return q * sign
def update_weights(self):
self.U.data = self.qr(self.U.data)
self.V.data = self.qr(self.V.data)
def forward(self, real, fake):
self.update_weights()
temp1 = real @ self.U
temp2 = real @ self.V
temp3 = fake @ self.U
temp4 = fake @ self.V
part1 = torch.trace(temp1 @ temp2.t()).mean()
part2 = torch.trace(temp3 @ temp4.t()).mean()
return part1 - part2