概
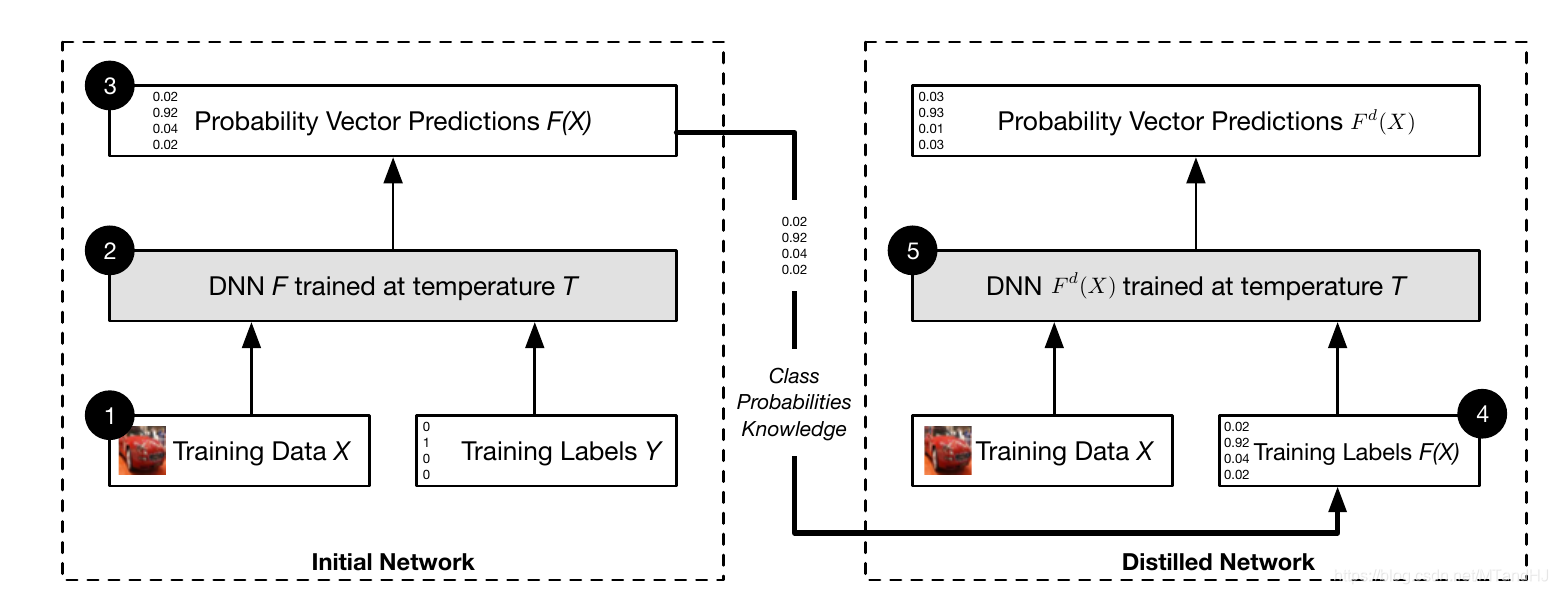
本文提出一种distillation model, 能够免疫大部分的adversarial attacks, 具有良好的鲁棒性, 同时容易训练.
主要内容
| 符号 | 说明 |
|---|---|
| (F(cdot)) | 神经网络, 且(F(X)=mathrm{softmax^*}(Z(X))). |
| (X in mathcal{X}) | 样本 |
| (Y) | 样本对应的标签 |
| (F^d) | distilled network |
| (T) | temperature |
注: 这里的(mathrm{softmax}^*(z)_i:=frac{e^{z_i/T}}{sum_j e^{e_j/T}}, i= 0,ldots, N-1);
注: (F^d)与(F)网络结构一样;
算法
Input: (T),训练数据((X,Y)).
- 在训练数据((X, Y))上训练得到(F);
- 得到新的训练数据((X, F(X)));
- 利用((X, F(X)))训练(F^d);
- 修改(F^d)的最后一层(T=1).
Output: (F^d).
为什么这个算法是有效的呢?
- 训练(F^d)用的标签是概率向量(F(X)), 拿数字举例, 如果写的草一点(7)和(1)是很相近的, 但如果训练的标签是((0,0,0,0,0,0,1,0,0,0))的话反而不符合实际, 会导致不稳定;
- 当(T)比较大的时候(训练):
[frac{partial F_i(X)}{partial X_j}|_T = frac{1}{T}frac{e^{z_i / T}}{g^2(X)}ig( sum_{l=1^N}(frac{partial z_i}{partial X_j}-frac{partial z_l}{partial X_j})e^{z_l /T}ig),
]
会比较小, 其中(g(X)=sum_{l=0}^{N-1} e^{z_l(X)/T}).
3. 在测试的时候, 我们令(T=1), 假设(X)在原先情况下(z_1/T)最大, (z_2/T)次大, 则
[epsilon=z_2/T-z_1/T= 0 + mathbf{Tr}(mathcal{G}^T delta X) + o(delta x),
]
则
[Tepsilon=z_2-z_1= 0 + T cdot mathbf{Tr}(mathcal{G}^T delta X) + o(delta x),
]
其中(mathcal{G})为(z_2-z_1)在(X)处的负梯度.
一些有趣的指标
鲁棒性定义
[
ho_{adv}(F)= E_{mu}[Delta_{adv}(X,F)],
]
其中(mu)为样本的分布
[Delta_{adv}(X,F) = arg min_{delta X} { | delta X| : F(X+delta X)
ot = F(X) }.
]
可采用下式来实际估计
[
ho_{adv}(F) approx frac{1}{|mathcal{X}|} sum_{X in mathcal{X}} min _{delta X} |delta X|.
]
合格的抗干扰机制
- 对原有结构有较少的影响;
- 网络对干净数据因具有相当的正确率;
- 较好的训练速度;
- 对(| delta X|)较小的情况能够免疫干扰.
原文还有一个理论分析, 但我认为不重要, 略过.
import torch.nn as nn
class Tsoftmax(nn.Module):
def __init__(self, T=100):
super(Tsoftmax, self).__init__()
self.T = T
def forward(self, x):
if self.train():
return nn.functional.softmax(x / self.T)
else:
return nn.functional.softmax(x)