Kingma D P, Welling M. Auto-Encoding Variational Bayes[J]. arXiv: Machine Learning, 2013.
主要内容
自编码, 通过引入Encoder和Decoder来估计联合分布(p(x,z)), 其中(z)表示隐变量(我们也可以让(z)为样本标签, 使得Encoder成为一个判别器).
在Decoder中我们建立联合分布(p_{ heta}(x,z))以估计(p(x,z)), 在Encoder中建立一个后验分布(q_{phi}(z|x))去估计(p_{ heta}(z|x)), 然后极大似然:
上式俩边关于(z)在分布(q_{phi}(z))下求期望可得:
既然KL散度非负, 我们极大似然(log p_{ heta}(x))可以退而求其次, 最大化(mathbb{E}_{q_{phi}(z|x)}(log frac{p_{ heta}(x,z)}{q_{phi}(z|x)} ))(ELBO, 记为(mathcal{L})).
又((p_{ heta}(z))为认为给定的先验分布)
我们接下来通过对Encoder和Decoder的一些构造进一步扩展上面俩项.
Encoder (损失part1)
Encoder 将(x ightarrow z), 就相当于在(q_{phi}(z|x))中进行采样, 但是如果是直接采样的话, 就没法利用梯度回传进行训练了, 这里需要一个重参化技巧.
我们假设(q_{phi}(z|x))为高斯密度函数, 即(mathcal{N}(mu, sigma^2 I)).
注: 文中还提到了其他的一些可行假设.
我们构建一个神经网络(f), 其输入为样本(x), 输出为((mu, log sigma))(输出(log sigma)是为了保证(sigma)为正), 则
其中(odot)表示按元素相乘.
注: 我们可以该输出为((mu, L))((L)为三角矩阵, 且对角线元素非负), 而假设(q_{phi}(z|x))的分量不独立, 其协方差函数为(L^TL), 则((z=mu + L epsilon)).
当(p_{ heta}(z)=mathcal{N}(0, I)), 我们可以显示表达出:
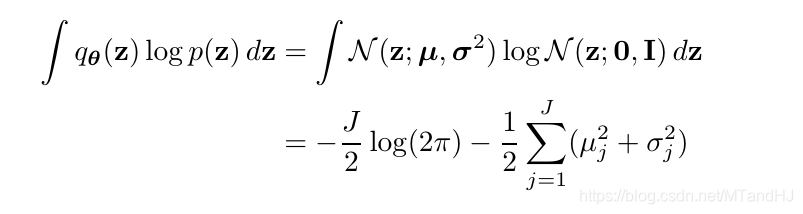
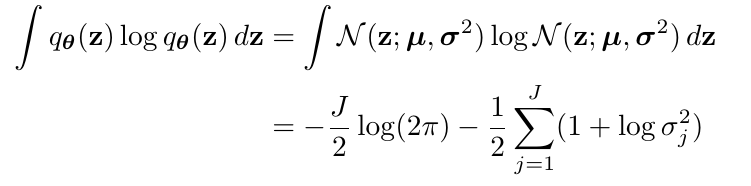
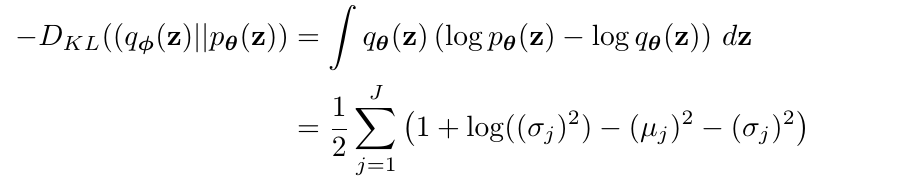
Decoder (损失part2)
现在我们需要处理的是第二项, 文中这地方因为直接设计(p_{ heta}(x,z))不容易, 在我看来存粹是做不到的, 但是又用普通的分布代替不符合常理, 所以首先设计一个网络(g_{ heta}(z)), 其输出为(hat{x}), 然后假设(p(x|hat{x}))的分布, 第二项就改为近似(mathbb{E}_{q_{phi}(z|x)}p_{ heta}(x|hat{x})).
这么做的好处是显而易见的, 因为Decoder部分, 我们可以通过给定一个(z)然后获得一个(hat{x}), 这是很有用的东西, 但是我认为这种不是很合理, 因为除非(g)是可逆的, 那么(p_{ heta}(x|z)= p _{ heta}(x|hat{x})) (当然, 别无选择).
伯努利分布
此时(hat{x}=g(z))是(x=1)的概率, 则此时第二项的损失为
为(二分类)交叉熵损失.
高斯分布
一种简单粗暴的, (p(x|hat{x})=mathcal{N}(hat{x},sigma^2 I)), 此时损失为类平方损失, 文中也有别的变换.
代码
import torch
import torch.nn as nn
class Loss(nn.Module):
def __init__(self, part2):
super(Loss, self).__init__()
self.part2 = part2
def forward(self, mu, sigma, real, fake, lam=1):
part1 = (1 + torch.log(sigma ** 2)
- mu ** 2 - sigma ** 2).sum() / 2
part2 = self.part2(fake, real)
return part1 + lam * part2