引
这篇论文比较短,先看了这篇,本来应该先把ADAGRAD看了的。普通的基于梯度下降的方法,普遍依赖于步长,起始点的选择,所以,受ADAGRAD的启发,作者提出了一种ADADELTA的方法。
其中(g_t=frac{partial f(x_t)}{partial x_t}),所以下一步迭代就是:
主要内容
ADAGRAD方法:
也就是,步长与之前所有的梯度有关,显然这个步长是会逐渐减少的。但是这个缺点也很明显,如果起始点的梯度很大,那么就会导致后续步长很小,而一开始的梯度很小,就会导致后续步长很大,产生振荡,有些怪怪的。
而ADADELTA希望只关心一部分的梯度,比如
但是这么做,每次迭代都必须记录(k)个梯度,这显得不怎么效率,于是,作者相处了一个法子:
可以看到,对于(g_1),(t+1)步之后其影响为:( ho^t(1- ho) g_1),对整个迭代造成的影响是一个等比序列:
最后趋向于:
这么做就俩劝其美啦。
记:
其中(epsilon)是为了让除法有意义而添加的小量。
所以
这还不是最终版本,另一个启发决定了(eta)的选择。
我们知道,很多问题是有实际含义的,(x)可能是有单位的,比如是米,天等,所以,一个很自然的期望是,(Delta x)的单位和(x)是保持一致的。但是:
也就是说(Delta x)的步长单位和梯度单位是一致的,就像是(l=vt),(Delta t)的步长单位是(m/s),是时间单位的倒数。
而利用二阶导数迭代步长就符合单位一致(如Newton方法):
其中(H)为Hessian矩阵。
又注意到:
于是,完全体的ADADELTA方法变为如下:
分子式(t-1)的原因式(Delta x_t)压根不知道,所木有办法,就将就一下。
算法
完整的算法如下:

需要注意一点的是,在实际实验中,我们设置(E[Delta x^2]_0=1)而不是如算法中所说的0。因为,如果设置为0,那么意味着第一步只进行相当微小的迭代,所以之后也都是微小的迭代。或许作者是将(epsilon)设置为(1)?而不是一个小量?
ADADELTA 代码
import numpy as np
import matplotlib.pyplot as plt
这次用比较怪一点的方式来写,首先,创建一个类,用来存放函数(f)和梯度(g)
class ADADELTA:
def __init__(self, function, gradient, rho=0.7):
assert hasattr(function, "__call__"), "Invalid function"
assert hasattr(gradient, "__call__"), "Invalid gradient"
assert 0 < rho < 1, "Invalid rho"
self.__function = function
self.__gradient = gradient
self.rho = rho
self.acc_gradient = 0 #初始化accumulate gradient
self.acc_updates = 1 #初始化accumulate updates
self.progress = []
@property
def function(self):
return self.__function
@property
def gradient(self):
return self.__gradient
def reset(self):
self.acc_gradient = 0 #初始化accumulate gradient
self.acc_updates = 1 #初始化accumulate updates
self.progress = []
计算累计梯度
def accumulate_gradient(self, gt):
self.acc_gradient = self.rho * self.acc_gradient
+ (1 - self.rho) * gt ** 2
return self.acc_gradient
ADADELTA.accumulate_gradient = accumulate_gradient
更新(E[Delta x]_t)
def accumulate_updates(self, deltax):
self.acc_updates = self.rho * self.acc_updates
+ (1 - self.rho) * deltax ** 2
return self.acc_updates
ADADELTA.accumulate_updates = accumulate_updates
计算更新步长:
def step(self, x, smoothingterm=1e-8):
gt = self.gradient(x)
self.accumulate_gradient(gt)
RMS_gt = np.sqrt(self.acc_gradient + smoothingterm)
RMS_up = np.sqrt(self.acc_updates + smoothingterm)
deltax = -RMS_up / RMS_gt * gt
self.accumulate_updates(deltax)
return x + deltax
ADADELTA.step = step
进行t步
def process(self, startx, t, smoothingterm=1e-8):
x = startx
for i in range(t):
self.progress.append(x)
x = self.step(x, smoothingterm)
return self.progress
ADADELTA.process = process
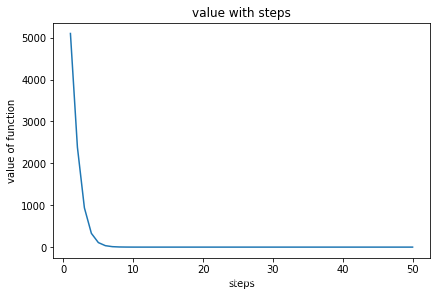
可视化
def plot(self):
x = np.arange(1, len(self.progress) + 1)
y = np.array([
self.function(item) for item in self.progress
])
fig, ax = plt.subplots(constrained_layout=True)
ax.plot(x, y)
ax.set_xlabel("steps")
ax.set_ylabel("value of function")
ax.set_title("value with steps")
plt.show()
ADADELTA.plot = plot
def function(x):
return x[0] ** 2 + 50 * x[1] ** 2
def gradient(x):
return 2 * x[0] + 100 * x[1]
test = ADADELTA(function, gradient, 0.9)
test.reset()
startx = np.array([10, 10])
test.process(startx, 50)
test.plot()