等式约束优化（可行点）

目录

• 策略一 消除等式约束
• 策略二 Newton方向
  • 另外一种解释
  • Newton减量——停止准则
  • 可行下降方法的算法
  • Newton方法和消除法

《Convex Optimization》

之前，讲的下降方法以及Newton方法都是在无约束条件的前提下的。这里讨论的是在等式约束（线性方程）的前提下讨论的。我们研究的是下面的凸优化问题：

[egin{array}{ll} minimize & f(x) \ s.t. & Ax=b end{array} ]

其中(f:mathbb{R}^n ightarrow mathbb{R}, A in mathbb{R}^{p imes n}, rank A = p<n)
请不要怀疑(rank A = p<n)条件的可靠性，否则，只需找出其线性无关组即可。而且，显然，如果(Ax=b)如果无解，那么优化问题同样无解。
通过对对偶问题，及KKT条件的分析，可以知道，该优化问题存在最优解的充要条件是，存在(v^* in mathbb{R}^p)满足：

[Ax^*=b, quad abla f(x^*) + A^Tv^*=0 ]

策略一 消除等式约束

我们首先确定矩阵(F in mathbb{R}^{n imes (n-p)})和向量(hat{x} in mathbb{R}^n)，用以参数化可行集：

[{x|Ax=b} = {Fz+hat{x}|z in mathbb{R}^{n-p} } ]

只需，(hat{x})为(Ax=b)的一个特解即可。(F)是值域为(A)的零空间的任何矩阵（满足(A(Fz)=0)，即(Fz)可以取得所有(Ax=0)的解）。于是等式约束问题就可以变为无约束问题：

[minimize quad widetilde{f}(z) = f(Fz+hat{x}) ]

我们也可以为等式约束构造一个最优的对偶变量(v^*):

[v^*=-(AA^T)^{-1}A abla f(x^*) ]

另外需要注意的是，如果(F)是一个消除矩阵，那么任意的(FT)同样也是合适的消除矩阵，其中(T in mathbb{R}^{(n-p) imes (n-p)})是非奇异的。

策略二 Newton方向

我们希望导出等式约束问题：

[egin{array}{ll} minimize & f(x) \ s.t. & Ax=b end{array} ]

在可行点(x)处䣌Newton方向(Delta x_{nt})，将目标函数换成在x附近的二阶泰勒近似：

[egin{array}{ll} minimize & hat{f}(x+v)=f(x)+ abla f(x)^{T}v + frac{1}{2}v^T abla^2 f(x) v \ s.t. & A(x+v)=b end{array} ]

注意上述问题时关于(v)的优化问题。
根据我们在文章开头提到的最优性条件，可以得到：

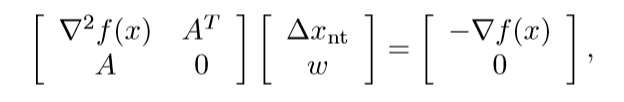
其中(Delta x_{nt})表示Newton方向，(w)是该二次问题的最优对偶变量。

另外一种解释

我们可以将Newton方向(Delta x_{nt})及其相关向量(w)解释为最优性条件

[Ax^*=b, quad abla f(x^*) + A^Tv^*=0 ]

的线性近似方程组的解。
我们用(x + Delta x_{nt})代替(x^*)，用(w)代替(v^*)，并将第二个方程中的梯度项换成其在(x)附近的线性近似，从而得到：

[A(x + Delta x_{nt})=b, quad abla f(x+Delta x_{nt})+A^Twapprox abla f(x) + abla^2 f(x) Delta x_{nt} + A^Tw = 0 ]

利用(Ax = b)，以上方程变成：

[ADelta x_{nt}=0, quad abla^2 f(x) Delta x_{nt} + A^Tw = - abla f(x) ]

这上面定义的一样。

Newton减量——停止准则

我们将等式约束问题的Newton减量定义为：

[lambda (x) = (Delta x_{nt}^T abla^2 f(x) Delta x_{nt})^{1/2} ]

这和无约束情况表示的是一样的，因此也可以进行同样的解释。
(f)在(x)处的二阶泰勒近似为：

[hat{f}(x+v) = f(x) + abla f(x)^T v + (1/2) v^T abla^2 f(x) v ]

(f(x))与二次模型之间的差值满足：

[f(x) - inf {hat{f}(x+v) | A(x+v) = b} = lambda (x)^2/2 ]

从上面可以看出，(lambda^2(x)/2)对(x)处的(f(x) - p^*)给出了基于二次模型的一个估计，这可以作为设计好的停止准则的基础。

可行下降方法的算法

注意，下面的算法初始点为可行点。

Newton方法和消除法

对原始问题采用Newton方法的迭代过程和对利用消除法简化后采用Newton方法过程完全一致，证明翻阅《凸优化》。