A.BowWow and the Timetable
•题意
给你一个二进制数，让你求小于这个数的所有4的幂的个数
•思路
第一反应是二进制与四进制转换
（其实不用真正的转换 QwQ）
由于二进制的两位对应四进制的一位
所以可以得到四进制下的位数
四进制的位数就是小于等于这个数的所有4的幂的个数，类比10进制下10的幂
由于不能有等于，所以根据二进制判断一下这个数是不是4的幂
因为12，1002，100002 ，二进制下4的幂除了首位的1，后面是偶数个0
所以判断是否是1带偶数个0，是的话个数减一
•代码
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=1e6+5; 4 char s[maxn]; 5 int main() 6 { 7 scanf("%s",s+1); 8 int len=strlen(s+1),flag=0; 9 int cnt=(len+1)/2; 10 for(int i=2;i<=len;i++) 11 if(s[i]=='0') flag++; 12 if(flag==len-1 && len&1) 13 cnt--; 14 printf("%d ",cnt); 15 }
B.Mislove Has Lost an Array
•题意
数组中只存在$1$或者$x$
$x$是偶数并且$x/2$必须在数组中存在
给定$l,r$数组中最少有$l$个不同的数，最多有$r$个不同的数
求数组里数的和的最小最大值
•思路
最小值是有$1,2,4...$等$l$个数，如果不足n个用$1$补齐
最大值是有$1,2,4...$等$r$个数，如果不足用这$r$个数中最大的补齐
•代码
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 int main() 5 { 6 int n,l,r; 7 cin>>n>>l>>r; 8 ll Min=0; 9 int cnt,i; 10 for(i=1,cnt=1;i<=l;cnt*=2,i++) 11 Min+=cnt; 12 Min+=(n-l); 13 14 ll Max=0; 15 for(cnt=1,i=1;i<=min(n,r);cnt*=2,i++) 16 Max+=cnt; 17 cnt/=2; 18 if(r<=n) 19 Max+=1ll*(n-r)*cnt; 20 cout<<Min<<' '<<Max<<endl; 21 }
C. Anna, Svyatoslav and Maps
•题意
给出邻接矩阵表示一个有向图
"1"代表有路，"0"代表没有路
给出长度为$m$的序列，表示一条最短路
求，这个序列的一个子序列s，
满足这个子序列s的最短路是m的序列，且s最短
•思路
由于从一个点到另一个点的路径可能不止一条
一旦固定了路径，那么从这个点到另一个点不必须经过的点如果在固定的路径中的话
就必须有，防止从其它点经过
二那些必须经过的点，就不用有了，因为要使长度最短
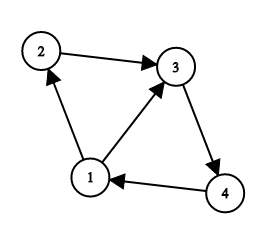
固定路径1,2,3,4
1可以直接到3而不必须经过2，但是固定路径里有2
所以2必须存在，才能使得经过1,2
2到4必须经过3，所以2->4路径有存在了3
为了使s最短，3不会有
•代码
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define inf 0x3f3f3f3f 4 const int maxn=1e6+5; 5 char s[105][105]; 6 int dis[105][105]; 7 int a[maxn],ans[maxn]; 8 int n,m; 9 10 void Init() 11 { 12 for(int i=1;i<=n;i++) 13 { 14 for(int j=1;j<=n;j++) 15 { 16 dis[i][j]=inf; 17 if(i==j) dis[i][j]=0; 18 if(s[i][j]=='1') dis[i][j]=1; 19 } 20 } 21 } 22 23 void floyd() 24 { 25 for(int k=1;k<=n;k++) 26 for(int i=1;i<=n;i++) 27 for(int j=1;j<=n;j++) 28 dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]); 29 } 30 31 int main() 32 { 33 scanf("%d",&n); 34 for(int i=1;i<=n;i++) 35 scanf("%s",s[i]+1); 36 Init(); 37 floyd(); 38 39 scanf("%d",&m); 40 for(int i=1;i<=m;i++) 41 scanf("%d",a+i); 42 43 int cnt=0; 44 ans[++cnt]=a[1];///首 45 int pre=a[1]; 46 for(int i=2;i<=m;i++) 47 { 48 int cur=a[i-1]; 49 int nex=a[i]; 50 if(pre==cur) 51 continue; 52 ///要不必须经过的点 53 ///不要必须经过的点 54 if(dis[pre][cur]+dis[cur][nex]!=dis[pre][nex]) 55 { 56 ans[++cnt]=cur; 57 pre=cur; 58 } 59 } 60 ans[++cnt]=a[m];///尾 61 62 printf("%d ",cnt); 63 for(int i=1;i<=cnt;i++) 64 printf("%d ",ans[i]); 65 puts(""); 66 }
D.Kirk and a Binary String
•题意
给你一个$01$字符串s，让你找到一个t串，使得
- t串与s串的区间所有单调非递减长度相同
- t串中0个数最多
•思路
对于一个字符串，当前位置有$0,1$两种情况
- 当前位置是0
当前位置是0，对于以他为起点的单调非递减子序列肯定有贡献，
如果变为1，大多数情况下长度会减小（除了0后面全是1的情况，011111长度不变）
如果变为1，0的数量比不变减少违背第二个任务
- 当前位置是1
如果变为0，对于以他(也就是以1) 为起点的单调非递减子序列来说，长度无影响
对于以0为起点的单调非递减子序列来说，长度会受到影响
既然想要更多的0，那就需要尽可能的把1 变成0，那如何才能没有影响呢?
那就需要以他(也就是以1) 为起点的单调非递减子序列的长度大于以0为起点的单调非递减子序列长度
因为影响大局的最长的那个，那就让即使小的变化了，也不会对大局产生影响！
换句话说，若想将$1$ 变为 $0$ ，必须保证后面所有的区间的单调非递减子序列长度必须和 1 的个数相等
也就是从后往前找，当$1$的个数大于$0$的个数时，$1$才可以变成$0$
•代码
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const int maxn=1e6+4; 5 char s[maxn]; 6 int a[maxn]; 7 int main() 8 { 9 scanf("%s",s+1); 10 int len=strlen(s+1); 11 int cnt=0; 12 for(int i=len;i>=1;i--) 13 { 14 if(s[i]=='0') 15 cnt++; 16 else 17 { 18 if(cnt) --cnt; 19 else s[i]='0'; 20 } 21 } 22 23 printf("%s",s+1); 24 }